Page 260 - Physical chemistry understanding our chemical world

PHASE EQUILIBRIA INVOLVING VAPOUR PRESSURE 227

80 000
70 000 Total vapour pressure
Partial pressure of octane/Pa 50 000 Vapour pressure Partial pressure of benzene/Pa
60 000

40 000
of benzene
30 000
20 000
10 000 Vapour pressure
of octane
0
0 0.2 0.4 0.6 0.8 1
Mole fraction of benzene
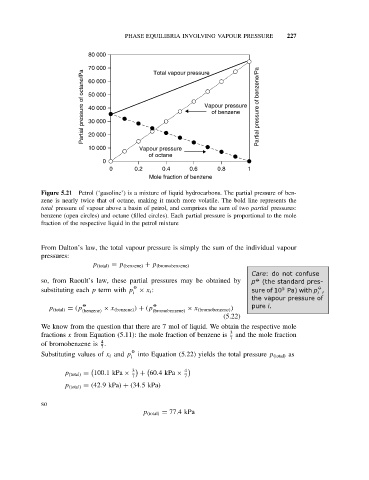
Figure 5.21 Petrol (‘gasoline’) is a mixture of liquid hydrocarbons. The partial pressure of ben-
zene is nearly twice that of octane, making it much more volatile. The bold line represents the
total pressure of vapour above a basin of petrol, and comprises the sum of two partial pressures:
benzene (open circles) and octane (filled circles). Each partial pressure is proportional to the mole
fraction of the respective liquid in the petrol mixture

From Dalton’s law, the total vapour pressure is simply the sum of the individual vapour
pressures:
p (total) = p (benzene) + p (bromobenzene)
Care: do not confuse
so, from Raoult’s law, these partial pressures may be obtained by p O (the standard pres-
O
5
O
substituting each p term with p × x i : sure of 10 Pa) with p ,
i i
the vapour pressure of
p (total) = (p O × x (benzene) ) + (p O × x (bromobenzene) ) pure i.
(benzene) (bromobenzene)
(5.22)
We know from the question that there are 7 mol of liquid. We obtain the respective mole
fractions x from Equation (5.11): the mole fraction of benzene is 3 and the mole fraction
7
4
of bromobenzene is .
7
O
Substituting values of x i and p into Equation (5.22) yields the total pressure p (total) as
i
3 4

p (total) = 100.1kPa × + 60.4kPa ×
7 7
p (total) = (42.9kPa) + (34.5kPa)
so
p (total) = 77.4kPa