Page 76 - Physical chemistry understanding our chemical world

PHYSICAL AND MOLECULAR INTERACTIONS 43

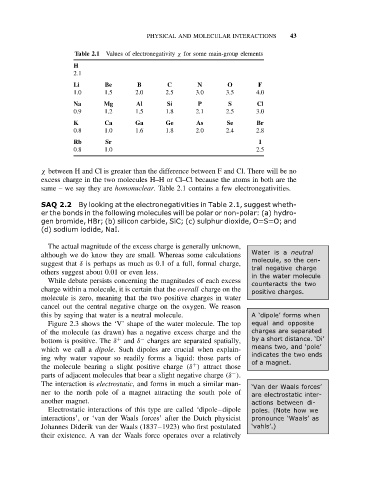
Table 2.1 Values of electronegativity χ for some main-group elements

H
2.1
Li Be B C N O F
1.0 1.5 2.0 2.5 3.0 3.5 4.0
Na Mg Al Si P S Cl
0.9 1.2 1.5 1.8 2.1 2.5 3.0
K Ca Ga Ge As Se Br
0.8 1.0 1.6 1.8 2.0 2.4 2.8
Rb Sr I
0.8 1.0 2.5

χ between H and Cl is greater than the difference between F and Cl. There will be no
excess charge in the two molecules H–H or Cl–Cl because the atoms in both are the
same – we say they are homonuclear. Table 2.1 contains a few electronegativities.

SAQ 2.2 By looking at the electronegativities in Table 2.1, suggest wheth-
er the bonds in the following molecules will be polar or non-polar: (a) hydro-
gen bromide, HBr; (b) silicon carbide, SiC; (c) sulphur dioxide, O=S=O; and
(d) sodium iodide, NaI.

The actual magnitude of the excess charge is generally unknown,
although we do know they are small. Whereas some calculations Water is a neutral
molecule, so the cen-
suggest that δ is perhaps as much as 0.1 of a full, formal charge,
tral negative charge
others suggest about 0.01 or even less. in the water molecule
While debate persists concerning the magnitudes of each excess
counteracts the two
charge within a molecule, it is certain that the overall charge on the positive charges.
molecule is zero, meaning that the two positive charges in water
cancel out the central negative charge on the oxygen. We reason
this by saying that water is a neutral molecule. A ‘dipole’ forms when
Figure 2.3 shows the ‘V’ shape of the water molecule. The top equal and opposite
of the molecule (as drawn) has a negative excess charge and the charges are separated
−
+
bottom is positive. The δ and δ charges are separated spatially, by a short distance. ‘Di’
means two, and ‘pole’
which we call a dipole. Such dipoles are crucial when explain-
indicates the two ends
ing why water vapour so readily forms a liquid: those parts of
of a magnet.
+
the molecule bearing a slight positive charge (δ ) attract those
−
parts of adjacent molecules that bear a slight negative charge (δ ).
The interaction is electrostatic, and forms in much a similar man-
‘Van der Waals forces’
ner to the north pole of a magnet attracting the south pole of are electrostatic inter-
another magnet. actions between di-
Electrostatic interactions of this type are called ‘dipole–dipole poles. (Note how we
interactions’, or ‘van der Waals forces’ after the Dutch physicist pronounce ‘Waals’ as
Johannes Diderik van der Waals (1837–1923) who first postulated ‘vahls’.)
their existence. A van der Waals force operates over a relatively