Page 231 - Physical Chemistry

lev38627_ch07.qxd 3/14/08 12:51 PM Page 212

212
Chapter 7 Suppose liquid water is placed in a closed container fitted with a piston, the sys-
One-Component Phase Equilibrium tem is heated to 300°C, and the system’s pressure is set at 0.5 atm. These T and P val-
and Surfaces
ues correspond to point R in Fig. 7.1. The equilibrium phase at R is gaseous H O, so
2
the system consists entirely of H O(g) at 300°C and 0.5 atm. If the piston pressure is
2
now slowly increased while T is held constant, the system remains gaseous until the
pressure of point S is reached. At S, the vapor starts to condense to liquid, and this
condensation continues at constant T and P until all the vapor has condensed. During
condensation, the system’s volume V decreases (Fig. 8.4), but its intensive variables
remain fixed. The amounts of liquid and vapor present at S can be varied by varying
V. After all the vapor has condensed at S, let the pressure of the liquid be increased
H 2 O isothermally to reach point Y. If the system is now cooled at constant pressure, its tem-
perature will eventually fall to the temperature at point I, where the liquid begins to
freeze. The temperature will remain fixed until all the liquid has frozen. Further cool-
ing simply lowers the temperature of the ice.
Suppose we now start at point S with liquid and vapor in equilibrium and
slowly heat the closed system, adjusting the volume (if necessary) to maintain the
presence of liquid and vapor phases in equilibrium. The system moves from point S
along the liquid–vapor line toward point C, with both T and P increasing. During
this process, the liquid-phase density decreases because of the thermal expansion of
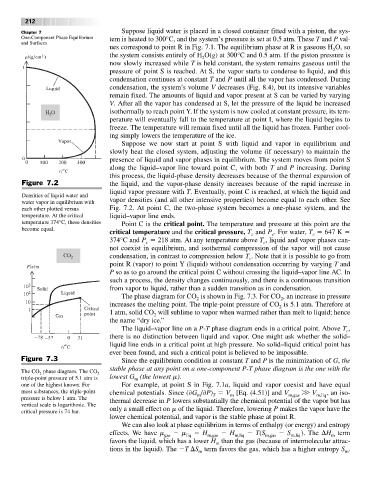
Figure 7.2 the liquid, and the vapor-phase density increases because of the rapid increase in
liquid vapor pressure with T.Eventually, point C is reached, at which the liquid and
Densities of liquid water and
water vapor in equilibrium with vapor densities (and all other intensive properties) become equal to each other. See
each other plotted versus Fig. 7.2. At point C, the two-phase system becomes a one-phase system, and the
temperature. At the critical liquid–vapor line ends.
temperature 374°C, these densities Point C is the critical point. The temperature and pressure at this point are the
become equal.
critical temperature and the critical pressure, T and P . For water, T 647 K
c
c
c
374°C and P 218 atm. At any temperature above T , liquid and vapor phases can-
c
c
not coexist in equilibrium, and isothermal compression of the vapor will not cause
condensation, in contrast to compression below T . Note that it is possible to go from
CO 2 c
point R (vapor) to point Y (liquid) without condensation occurring by varying T and
P so as to go around the critical point C without crossing the liquid–vapor line AC. In
such a process, the density changes continuously, and there is a continuous transition
from vapor to liquid, rather than a sudden transition as in condensation.
The phase diagram for CO is shown in Fig. 7.3. For CO , an increase in pressure
2
2
increases the melting point. The triple-point pressure of CO is 5.1 atm. Therefore at
2
1 atm, solid CO will sublime to vapor when warmed rather than melt to liquid; hence
2
the name “dry ice.”
The liquid–vapor line on a P-T phase diagram ends in a critical point. Above T ,
c
there is no distinction between liquid and vapor. One might ask whether the solid–
liquid line ends in a critical point at high pressure. No solid–liquid critical point has
ever been found, and such a critical point is believed to be impossible.
Figure 7.3 Since the equilibrium condition at constant T and P is the minimization of G, the
stable phase at any point on a one-component P-T phase diagram is the one with the
The CO phase diagram. The CO 2
2
triple-point pressure of 5.1 atm is lowest G (the lowest m).
m
one of the highest known. For For example, at point S in Fig. 7.1a, liquid and vapor coexist and have equal
most substances, the triple-point chemical potentials. Since ( G / P) V [Eq. (4.51)] and V m,gas W V m,liq , an iso-
m
T
m
pressure is below 1 atm. The thermal decrease in P lowers substantially the chemical potential of the vapor but has
vertical scale is logarithmic. The
critical pressure is 74 bar. only a small effect on m of the liquid. Therefore, lowering P makes the vapor have the
lower chemical potential, and vapor is the stable phase at point R.
We can also look at phase equilibrium in terms of enthalpy (or energy) and entropy
effects. We have m gas m liq H m,gas H m,liq T(S m,gas S m,liq ). The H term
m
favors the liquid, which has a lower H than the gas (because of intermolecular attrac-
m
tions in the liquid). The T S term favors the gas, which has a higher entropy S .
m
m