Page 329 - Physical Chemistry

lev38627_ch10.qxd 3/14/08 1:07 PM Page 310

310
Chapter 10 Summary
Nonideal Solutions
For a solution of n moles of the strong electrolyte M X in the solvent A, we defined
i n n
the chemical potential m of the electrolyte as a whole by m 10G>0n 2 and
i
i
i T,P,n A
found that m n m n m , where m and m are the chemical potentials of

i

g the cation and anion. The electrolyte’s chemical potential in solution was found to be

m m° nRT ln (n g m /m°), where n n n , n is defined by (n )
n

i
i
i
(n ) (n ) , and the mean molal ionic activity coefficient g is defined by (g )
n
n
n

(g ) (g ) .
n
n

10.6 DETERMINATION OF ELECTROLYTE
ACTIVITY COEFFICIENTS
The Gibbs–Duhem equation was used in Sec. 10.3 to find the activity coefficient of a
nonvolatile nonelectrolyte solute from known values of the solvent activity coefficient;
see Eq. (10.23). A similar procedure applies to a solution of a nonvolatile electrolyte.
We restrict the discussion to a solution of a single strong nonvolatile electrolyte i with
the formula M X .
n n
The solvent’s chemical potential can be written as m m* RT ln a , where
A A A
the mole-fraction scale is used [Eq. (10.39)]. This expression for m is the same as
A
g (10.4) and (10.7). Therefore, the vapor-pressure equation (10.13), which follows from

(10.4) and (10.7), holds for the solvent in an electrolyte solution:
P a P* ideal vapor, P not very high (10.56)
A
A A
Since the electrolyte solute is assumed nonvolatile, P equals the vapor pressure of the
A
solution, and (10.56) allows the solvent activity and activity coefficient to be found
from vapor-pressure measurements. Substitution of the constant-T-and-P differentials
dm [found from (10.39)] and dm [found from (10.51)] into the Gibbs–Duhem equa-
A i
tion (10.55) followed by integration then allows the electrolyte’s mean activity coeffi-
cient g in (10.51) to be found as a function of composition from the known solvent

activity coefficient as a function of composition. Electrolyte activity coefficients can
also be found from galvanic-cell data; Sec. 13.9.
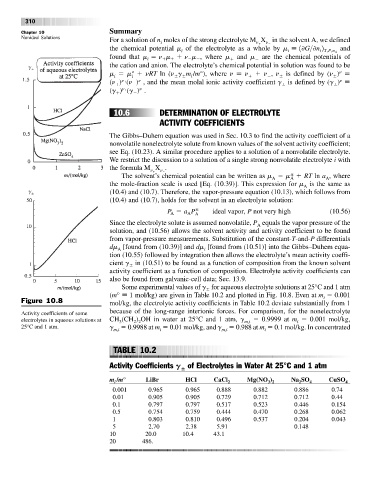
Some experimental values of g for aqueous electrolyte solutions at 25°C and 1 atm

(m° 1 mol/kg) are given in Table 10.2 and plotted in Fig. 10.8. Even at m 0.001
i
Figure 10.8 mol/kg, the electrolyte activity coefficients in Table 10.2 deviate substantially from 1
because of the long-range interionic forces. For comparison, for the nonelectrolyte
Activity coefficients of some
electrolytes in aqueous solutions at CH (CH ) OH in water at 25°C and 1 atm, g m,i 0.9999 at m 0.001 mol/kg,
i
3
2 2
25°C and 1 atm. g 0.9988 at m 0.01 mol/kg, and g 0.988 at m 0.1 mol/kg. In concentrated
m,i i m,i i
TABLE 10.2
Activity Coefficients G of Electrolytes in Water At 25°C and 1 atm

m /m° LiBr HCl CaCl 2 Mg(NO ) Na SO 4 CuSO 4
2
i
3 2
0.001 0.965 0.965 0.888 0.882 0.886 0.74
0.01 0.905 0.905 0.729 0.712 0.712 0.44
0.1 0.797 0.797 0.517 0.523 0.446 0.154
0.5 0.754 0.759 0.444 0.470 0.268 0.062
1 0.803 0.810 0.496 0.537 0.204 0.043
5 2.70 2.38 5.91 0.148
10 20.0 10.4 43.1
20 486.