Page 343 - Physical Chemistry

lev38627_ch10.qxd 3/14/08 1:07 PM Page 324

324
Chapter 10 Liquid–Vapor Equilibrium
Nonideal Solutions The expression for m in a nonideal gas mixture is obtained by replacing P in the
i i
ideal-gas-mixture m with f . Therefore, to take gas nonideality into account, all the
i i
pressures and partial pressures in the liquid–vapor equilibrium equations of Sec. 10.3
are replaced by fugacities. For example, the partial vapor pressures of a solution are
l
given by P g x P* [Eq. (10.14)] if the vapor is ideal. For nonideal vapor, this
i I,i i i
equation becomes
CH at
4
50ºC f g x f *
l
I,i i
i
i
where f*is the fugacity of the vapor in equilibrium with pure liquid i at the tempera-
i
l
ture of the solution, x and g are the mole-fraction and Convention I activity coeffi-
i I,i
cient of i in the solution, and f is the fugacity of i in the nonideal gas mixture in equi-
i
librium with the solution. For the pressure range of zero to a few atmospheres, the
truncated virial equation V RT/P B [Eq. (8.7) and the paragraph after (8.11)] is
m
widely used to correct for gas nonideality in liquid–vapor studies.
10.11 SUMMARY
The all-important chemical potentials m of components of a nonideal solid or liquid
i
solution are expressed in terms of activities and activity coefficients. One defines a
standard state for each component i and then defines its activity a so that m m°
i i i
RT ln a , where m° is the standard-state chemical potential of i.
i i
All standard states are at the T and P of the solution. If the mole-fraction scale is
used, the activity a is expressed as a g x , where g is the mole-fraction activity co-
i i i i i
efficient. Two different choices of mole-fraction standard states give Convention I and
Convention II. Convention I (used for mixtures of two liquids) takes the standard state
of each component as the pure component. Convention II (used for solutions of a solid
or gas solute in a liquid solvent) takes the solvent standard state as the pure solvent
and takes each solute standard state as the fictitious state of pure solute with solute
molecules experiencing the same intermolecular forces they experience in the infi-
nitely dilute solution. If the molality scale is used, each solute activity is a
m,i
g m /m°, where g is the molality-scale activity coefficient; the solvent activity is
m,i i m,i
a g x ; the solute standard state is the fictitious state with g 1 and m 1
A A A m,i i
mol/kg; the solvent standard state is the pure solvent. The molar concentration scale
is similar to the molality scale, but with c used instead of m .
i i
For Convention I, the activity coefficient g of substance i goes to 1 as the solu-
I,i
tion becomes pure i. For Convention II, the molality scale, and the molar concentra-
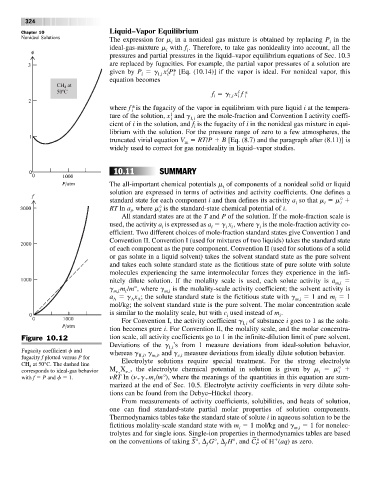
Figure 10.12 tion scale, all activity coefficients go to 1 in the infinite-dilution limit of pure solvent.
Deviations of the g ’s from 1 measure deviations from ideal-solution behavior,
I,i
Fugacity coefficient f and whereas g , g , and g measure deviations from ideally dilute solution behavior.
fugacity f plotted versus P for II,i m,i c,i
CH at 50°C. The dashed line Electrolyte solutions require special treatment. For the strong electrolyte
4
corresponds to ideal-gas behavior M X , the electrolyte chemical potential in solution is given by m m°
i
i
n
n
with f P and f 1. nRT ln (n g m /m°), where the meanings of the quantities in this equation are sum-

i
marized at the end of Sec. 10.5. Electrolyte activity coefficients in very dilute solu-
tions can be found from the Debye–Hückel theory.
From measurements of activity coefficients, solubilities, and heats of solution,
one can find standard-state partial molar properties of solution components.
Thermodynamics tables take the standard state of solute i in aqueous solution to be the
fictitious molality-scale standard state with m 1 mol/kg and g 1 for nonelec-
i m,i
trolytes and for single ions. Single-ion properties in thermodynamics tables are based

on the conventions of taking S°, G°, H°, and C° of H (aq) as zero.
f f P