Page 136 - Plastics Engineering

Mechanical Behaviour of Plastics 119

Therefore, using equation (2.75)

t -0.1
= (2.4 x
[E(t)l~* = 0.78t-'.'

The modulus at Tz(= 60°C) can now be calculated at any desired time. For
example, at 1 year (t = 3.15 x lo6 s)

[E(t)]m = 0.78(3.15 x lo6)-'.'
= 0.14 GN/m2

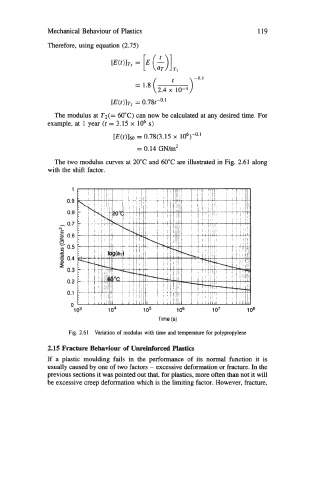
The two modulus curves at 20°C and 60°C are illustrated in Fig. 2.61 along
with the shift factor.

1
0.9
0.8

0.7
N
E
f 0.6
f - 0.5
1 0.4
5
0.3
0.2
0.1

0
1

Fig. 2.61 Variation of modulus with time and temperature for polypropylene

2.15 Fracture Behaviour of Unreinforced Plastics
If a plastic moulding fails in the performance of its normal function it is
usually caused by one of two factors - excessive deformation or fracture. In the
previous sections it was pointed out that, for plastics, more often than not it will
be excessive creep deformation which is the limiting factor. However, fracture,