Page 132 - Plastics Engineering

Mechanical Behaviour of Plastics 115

substituting from equations (2.73) and (2.74) once again
+
=
3aoiweW+s) + tlaoeW+s) ~((1 + t2)iw~oe~~~ 41t2&0eiwr
Dividing across by EOeiwr and letting E* = qei(wr+')/qgid

then, E* = v(t1 + t2)iw + tit2
t1 + tloi
Multiplying top and bottom by the conjugate of the denominator, we get

E* = (-532 + 02(h + t2'2)w2) + (t204i
6: + W2V2
and since E* = El + iE2,

storage modulus, E1 =

loss modulus, E2 =
_- t:w
E2
tans = -
E1 ,E%* + 3201 + h)m2
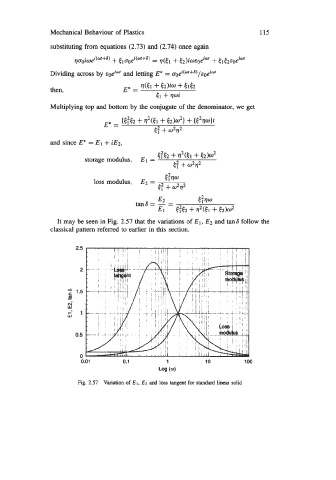
It may be seen in Fig. 2.57 that the variations of E 1, E2 and tan 6 follow the
classicai pattern referrid to earlier in this section.

2.5

2

z 1.5
g 1
w

0.5

0
0.01 0.1 1 10 100
Log (4
Fig. 2.57 Variation of E,, Et and loss tangent for standard linear solid