Page 128 - Plastics Engineering
P. 128
111
Mechanical Behaviour of Plastics I
T
-1
0 100 200 300 400 500 600 700 800
at
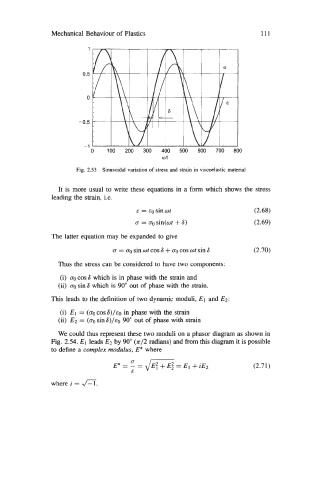
Fig. 2.53 Sinusoidal variation of stress and strain in viscoelastic material
It is more usual to write these equations in a form which shows the stress
leading the strain, i.e.
E = €0 sin wt (2.68)
a = 00 sin(wt + 6) (2.69)
The latter equation may be expanded to give
o = 00 sin wt cos 6 + a0 coswt sin S (2.70)
Thus the stress can be considered to have two components:
(i) 00 cos S which is in phase with the strain and
(ii) a0 sin6 which is 90" out of phase with the strain.
This leads to the definition of two dynamic moduli, El and E2:
(i) E1 = (00 cos S)/EO in phase with the strain
(ii) E:! = (00 sin S)/EO 90" out of phase with strain
We could thus represent these two moduli on a phasor diagram as shown in
Fig. 2.54. E1 leads E2 by 90" (n/2 radians) and from this diagram it is possible
to define a complex modulus, E* where
where i = a.