Page 337 - Power Electronics Handbook

Output voltage control 327

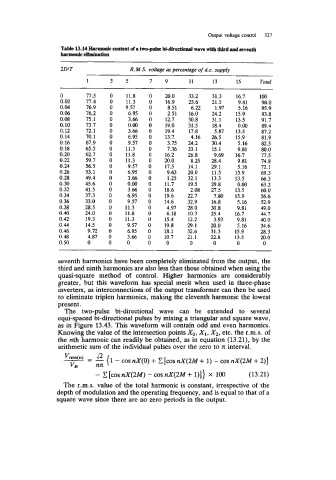
TPMC 13.14 tfumonlf content of a two-pulne bi.direetiolul wave with third .ad seventh
bprmoaie dhninstlon
2DIT R. M.S. voltage as percentage of d.c. supply

1 3 5 7 9 11 13 15 Total

0 77.5 0 11.8 0 20.0 33.2 31.3 16.7 100
0.02 77.4 0 11.3 0 16.9 25.6 21.5 9.81 98.0
0.04 76.9 0 9.57 0 8.51 6.22 1.97 5.16 95.9
0.06 76.2 0 6.95 0 2.51 16.0 24.2 15.9 93.8
0.08 75.1 0 3.66 0 12.7 30.8 31.1 13.5 91.7
0.10 73.7 0 0.00 0 19.0 31.5 18.4 0.00 89.4
0.12 72.1 0 3.66 0 19.4 17.8 5.87 13.5 87.2
0.14 70.1 0 6.95 0 13.7 4.16 26.5 15.9 81.9
0.16 67.9 0 9.57 0 3.75 24.2 30.4 5.16 82.5
0.18 65.5 0 11.3 0 7.36 33.1 15.1 9.81 80.0
0.20 62.7 0 11.8 0 16.2 26.8 9.69 16.7 77.5
0.22 59.7 0 11.3 0 20.0 8.25 28.4 9.81 74.8
0.24 56.5 0 9.57 0 17.5 14.1 29.1 5.16 72.1
0.26 53.1 0 6.95 0 9.63 20.0 11.5 15.9 69.3
0.28 49.4 0 3.66 0 1.25 32.1 13.3 13.5 66.3
0.30 45.6 0 0.00 0 11.7 19.5 29.8 0.00 63.2
0.32 41.5 0 3.66 0 18.6 2.08 27.5 13.5 60.0
0.34 37.3 0 6.95 0 19.6 22.7 7.80 15.9 56.6
0.36 33.0 0 9.57 0 14.6 32.9 16.8 5.16 52.9
0.38 28.5 0 11.3 0 4.97 28.0 30.8 9.81 49.0
0.40 24.0 0 11.8 0 6.18 10.3 25.4 16.7 44.7
0.42 19.3 0 11.3 0 15.4 12.2 3.93 9.81 40.0
0.44 14.5 0 9.57 0 19.8 29.1 20.0 5.16 34.6
0.46 9.72 0 6.95 0 18.1 32.6 31.3 15.9 28.3
0.48 4.87 0 3.66 0 10.7 21.1 22.8 13.5 20.0
0.50 0 0 0 0 0 0 0 0 0

seventh harmonics have been completely eliminated from the output, the
third and ninth harmonics are also less than those obtained when using the
quasi-square method of control. Higher harmonics are considerably
greater, but this waveform has special merit when used in three-phase
inverters, as interconnections of the output transformer can then be used
to eliminate triplen harmonics, making the eleventh harmonic the lowest
present.
The two-pulse bi-directional wave can be extended to several
equi-spaced bi-directional pulses by mixing a triangular and square wave,
as in Figure 13.43. This waveform will contain odd and even harmonics.
Knowing the value of the intersection points Xo, XI, X2, etc. the r.m.s. of
the nth harmonic can readily be obtained, as in equation (13.21), by the
arithmetic sum of the individual pulses over the zero to n interval.
-=- VrmS(") J2 { 1 - cos nX(0) + c [cos nX(2M + 1) - cos nX(2M + 211
VB nn
- [cos nX(2M) - cos nX(2M + l,]} x 100 (13.21)
The r.m.s. value of the total harmonic is constant, irrespective of the
depth of modulation and the operating frequency, and is equal to that of a
square wave since there are no zero periods in the output.