Page 506 - Practical Design Ships and Floating Structures

48 1

Michell, J. H.(1898), The Wave Resistance of a Ship, Phil. Mug., London, England,vol. 45, pp. 106-
123.
Newman, J. N. (1976), Linearized Wave Resistance Theory, Proc. Znt. Sem. on Wave Resistance,
-
pp.3 1-43. SOC. Nav. Arch. of Japan, Tokyo.
Newman, J. N. (1987), Evaluation of the Wave-Resistance Green Function: Part 1-The Double
Integral. J. Ship Res. 3 1 : 2, June, pp. 79-90.
Tuck, E. 0. (1966), Shallow Water Flows Past Slender Bodies. J. FZuidMech. 26, pp. 89-95.
Wehausen, J. V. and Laitone, E.V.(1960), Surface Waves in Handbuch der Physik, Springer-Verlag,
Berlin, Vol. 9, 446-778.
Wigley, W.C.S.(1942), Calculated and Measured Wave Resistance on a Series of Forms Defined
Algebraically. Trans. RINA, Vol. 84,52.

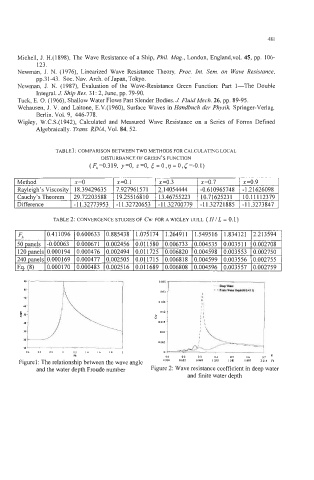
TABLE1 : COMPARISON BETWEEN TWO METHODS FOR CALCULATING LOCAL
DISTURBANCE OF GREEN’S FUNCTION
(F,,=0.319, y=O, z=O, &O,v=O,<=-O.l)

Method x =o x=o.1 x=0.3 x=0.7 x=0.9
Rayleigh’s Viscosity 18.39429635 7.927961571 2.14054444 -0.610965748 -1.21626098
Cauchy’s Theorem 29.72203588 19.25516810 13.46755223 10.71625231 10.111 12379
Difference -1 1.32773953 -1 1.32720653 -1 1.32700779 -1 1.32721885 -1 1.3273847

TABLE 2: CONVERGENCE STUDIES OF Cw FOR A WIGLEY UULL ( HI L = 0.1)

0 035
0 03
0.025
0 02
8
0.01s I \
r\l “L
0 01
0 ws
I . , , , . .