Page 87 - Pressure Swing Adsorption

62 PRESSURE SWING ADSORPTION FUNDAMENTALS OF ADSORPTION 63

2.48; so it 1s evident thai the temperature profile will propagate with a wave
velocity given by:
12 80
I
I
Temperature
70 (2.68)
IO
60 where da"' /dT represents the temperature dependence of the equilihnum
loading. ln effect heat behaves as an addit1onai componcnc m the system with
's 8 50 \,' its own charactenst1c propagation velocity. Since the,adsorpiion equilibna for
,. _,... ,. all soectes are temperature dependent. it 1s evident that a temoerature
.;
X
5
0 ~ co,
~ 6 40 :;; transition will in generai cause changes in concentration levels of all species.
~ 0
-" E The only exception arises when the velocity of the temperature front is faster
w
0
::, ~ than that of all concentratton fronts. In that situation. which 1s m fact quite
30
4 common for adsorption of light gases at ambient temperature and pressure, a
"pure thermal wave" will he formed and will pass through the column ahead
20 of all concentration changes.
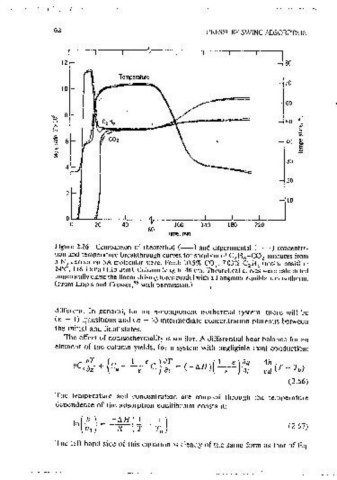
2 An example showing the form of the effluent coricentration and temoera-
10 ture curves for a two-component (olus carrier) adiabatJC system is given m
Figure 2.26. The least strongly adsorbed soec1es (ethane) passes most raoidlv
0 through the column, emerging as a relatively sharo constant pattern front.
0 20 40 100 140 180 220
60 The ethane concentration rises well above the feed concentration level as a
Time, mm resuit of displacement by the slowcr-rnovmg carbon dioxide. The second
Figure 2.26 Comoanson of theoretical (--) and experimental (- - •) concentra- front (due to actsorptlon of carbon dioxide) 1s also sharp and 1s accompanied
tion and temperature breakthrough curves for somtion of C H -CO mixtures from by a simultaneous decrease m ethane concentrat1on. The final front 1s due to
2 6 2
a Nl earner on 5A molecular sieve. Feed: 10.5% CO . 7.03% C H.., (molar basis) at
2 2 the thermal wave; which in this system propagates more siowly than either of
24"C. I 16.5 kPa ( 1.15 atm). Column length, 48 cm. Theoretical curves were calculated the mass transfer fronts. This third front is of proportional pattern form and
numencally using the linear driving force model with a Langmuir eouilibnum isotherm.
(From Liapis and Crosser, 53 with oenmss1on.) 1s accompamed by simultaneous changes m the concentrations of both ethane
1
and carbon dioxide, resuiting from the temperature dependence of the
eauilibrium isotherms. A numencal s1mulat1on based on the simultaneous
different. In general, for an n-component 1sotherrnal system, there will be solution of the differential heat and mass balance equations (Eqs. 2.66 and
(n - 1) transitions and (n - 2) intermediate concentration plateaus between 2.53) with a simple lineanzed rate expression (Eq. 2.57), and a Langmuir
the initial and final states. eouilibnum isotherm (Ea. 2.13) provides a very good representation of the
observed behavtor.
The effect of nonisothermality is similar. A differential heat baiance for an
element of the column yields, for a system with negligible axial conduction:
1 1
,-c,~; +(c.+ ~•c,)~~ -(-LiHJ( ~•)~; -;;cT-T ) References
0
(2.66) I. D. M. Ruthven, Principles of Adsorption and Adsorptwn Processes. John Wiley, New York
(1984).
The temperature and concentration are coupled through the temperature
2. R. T. Yang, Gas Separation by Adsorpt/Ofl Processes, Butterworth, Stoneham, MA (1987).
dependence of the adsorption eouilibrium constant:
3. M. Suzuki, Adsorplwn En,:meerm,:, Kodansha Elsevier. Tokvo (19CJO).
(2.67) 4. Y. Matsumurn, /'roe. h·t J11dia11 Carho11 C(Jnference, New Delhi, pp. (J 1 J--]IJ6(!91S2).
5. K. Chihara and M. Suzuki. Carbon 17, 339 (1979).
The ieft-hand side of this equation is clcariy of the same form as that of Eq. 6. J. Koresh and A. Soffer, J. Chem .. foe. Fa,U(/av Truns. ! 76, 2457 (19~01.