Page 165 - Principles of Applied Reservoir Simulation 2E

150 Principles of Applied Reservoir Simulation

A problem with large timesteps in the fully implicit technique is the
introduction of a numerical effect known as numerical dispersion [Lantz, 1971;
Fanchi, 1983]. Numerical dispersion is introduced when the Taylor series
approximation is used to replace derivatives with finite differences. The resulting
truncation error introduces an error in calculating the movement of saturation
fronts that looks like physical dispersion, hence it is called numerical dispersion.
Numerical dispersion arises from time and space discretizations that lead
to smeared spatial gradients of saturation or concentration [Lantz, 1971] and grid
orientation effects [Fanchi, 1983; and Chapter 16]. The smearing of saturation
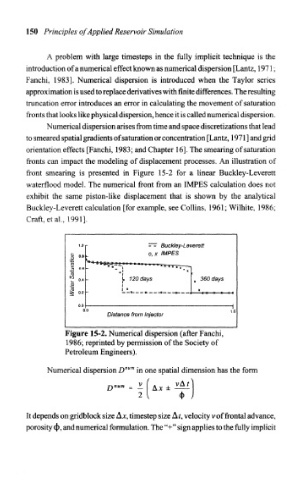
fronts can impact the modeling of displacement processes. An illustration of
front smearing is presented in Figure 15-2 for a linear Buckley-Leverett
waterflood model. The numerical front from an IMPES calculation does not
exhibit the same piston-like displacement that is shown by the analytical
Buckley-Leverett calculation [for example, see Collins, 1961; Wilhite, 1986;
Craft, etal, 1991].

10 r — Buckley-Leverett
o, x IMPES
.o 0.6
^*-*&.j-» » ii i^n n
5 " " " • • A j t ^ z
2 0 6 " »' * *
CD
CO |, 120 days 360 days
0.4 x
i
"S.
m 1 ° X
0.2
0,0 i 0
Distance from Injector
Figure 15-2. Numerical dispersion (after Fanchi,
1986; reprinted by permission of the Society of
Petroleum Engineers).

num
Numerical dispersion D in one spatial dimension has the form

It depends on gridblock size A*, timestep size A/, velocity v of frontal advance,
porosity (|>, and numerical formulation. The "+" sign applies to the fully implicit