Page 84 - Probability and Statistical Inference

1. Notions of Probability 61

1.7.9 In this exercise, you are given the expressions of the pdf of different
random variables. In each case, identify the random variable by its standard
name and specify the values of the associated parameters. Also, find the value
of c in each case.
(i) f(x) = cexp(–πx)I(x > 0), c is a positive constant;
2
(ii) f(x) = cexp(–πx ), x ∈ ℜ, and c is a positive constant;
2
(iii) f(x) = cexp(–x – 1/4x), x ∈ ℜ, and c is a positive constant;
(iv f(x) = 4x exp(–2x)I(x > 0), c is a positive constant;
c
(v) f(x) = 128/3x exp(–cx)I(x > 0), c is a positive constant;
4
(vi) f(x) = 105x (1 – x) I(0 < x < 1), c is a positive constant.
c
4
1.7.10 Suppose that a random variable X has the Gamma(2, 1) distribution
with its pdf given by (1.7.20). Find the expressions for P(X < a), P(X > b) in the
simplest form where a, b are positive numbers. {Hint: Observe that
and evaluate this integral by parts.}
1.7.11 Suppose that a random variable X has the Gamma(3, 2) distribution
with its pdf given by (1.7.20). Find the expressions for P(X < a), P(X > b) in
the simplest form where a, b are positive numbers. {Hint: Observe that P(X
< a) = 1/16 x2 e dx and evaluate this integral by parts.}
-x/2
1.7.12 Suppose that a random variable X has the distribution. Derive
the expression of the associated df explicitly. Also, find P(X > a + b | X > a)
where a, b are positive numbers. Does this answer depend on the number a?
Explain.

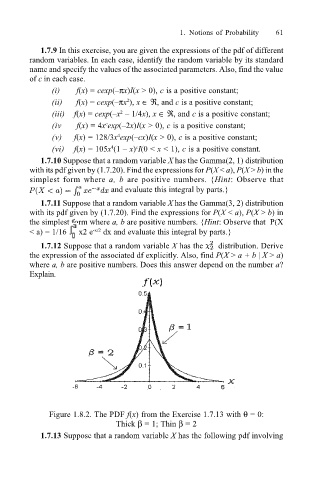
Figure 1.8.2. The PDF f(x) from the Exercise 1.7.13 with θ = 0:
Thick β = 1; Thin β = 2
1.7.13 Suppose that a random variable X has the following pdf involving