Page 178 - Radar Technology Encyclopedia

error, multipath error, platform-dependent 168

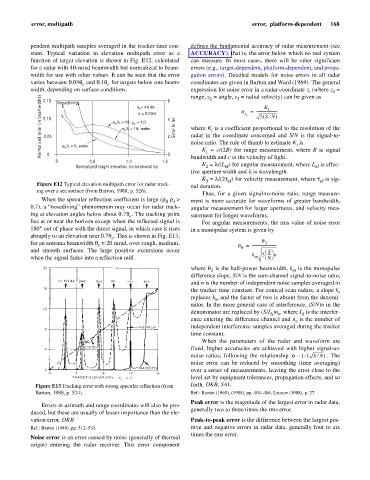
pendent multipath samples averaged in the tracker time con- defines the fundamental accuracy of radar measurement (see
stant. Typical variation in elevation multipath error as a ACCURACY); that is, the error below which no real system
function of target elevation is shown in Fig. E12, calculated can measure. In most cases, there will be other significant
for a radar with 40-mrad beamwidth but normalized to beam- errors (e.g., target-dependent, platform-dependent, and propa-
width for use with other values. It can be seen that the error gation errors). Detailed models for noise errors in all radar
varies between 0.05q and 0.1q for targets below one beam- coordinates are given in Barton and Ward (1969). The general
e
e
width, depending on surface conditions. q e = 40 mr 6 expression for noise error in a radar coordinate z (where z =
1
i
range, z = angle, z = radial velocity) can be given as
Normalized error (in beamwidths) 0.10 - s h /l = 15, r o = 1.0 4 2 Error in mr where K is a coefficient proportional to the resolution of the
3
2
0.15
Nosediving
K
i
-----------------------
s =
l = 0.03m
2 SN )
(
z i
¤
/l = 15, water
i
s h
radar in the coordinate concerned and S/N is the signal-to-
0.05
noise ratio. The rule of thumb to estimate K is
K = c/(2B) for range measurement, where B is signal
1
0
0 s h /l = 5, water 0.5 1.0 1.5 0 bandwidth and c is the velocity of light. i
ef
ef
2
Normalized target elevation (in beamwidths) K = l/(L ) for angular measurement, where L is effec-
tive aperture width and l is wavelength.
K = l/(2t ) for velocity measurement, where t is sig-
3
ef
ef
Figure E12 Typical elevation multipath error for radar track- nal duration.
ing over a sea surface (from Barton, 1988, p. 526).
Thus, for a given signal-to-noise ratio, range measure-
When the specular reflection coefficient is large (r r >
0 s ment is more accurate for waveforms of greater bandwidth,
0.7), a “nosediving” phenomenon may occur for radar track- angular measurement for larger apertures, and velocity mea-
ing at elevation angles below about 0.7q. The tracking point surement for longer waveforms.
e
lies at or near the horizon except when the reflected signal is For angular measurements, the rms value of noise error
180° out of phase with the direct signal, in which case it rises in a monopulse system is given by
abruptly to an elevation near 0.7q. This is shown in Fig. E13,
e
q
for an antenna beamwidth q = 20 mrad, over rough, medium, s = ---------------------------
3
e
and smooth surfaces. The large positive excursions occur q S
æö
k 2 ---- n
when the signal fades into a reflection null. m èø
N
where q is the half-power beamwidth, k is the monopulse
3
m
difference slope, S/N is the sum-channel signal-to-noise ratio,
and n is the number of independent noise samples averaged in
the tracker time constant. For conical-scan radars, a slope k s
replaces k and the factor of two is absent from the denomi-
m
nator. In the more general case of interference, (S/N)n in the
denominator are replaced by (S/I )n , where I is the interfer-
D e
D
ence entering the difference channel and n is the number of
e
independent interference samples averaged during the tracker
time constant.
When the parameters of the radar and waveform are
fixed, higher accuracies are achieved with higher signal-to-
¤
. The
noise ratios, following the relationship s 1 (¤~ SN )
noise error can be reduced by smoothing (time averaging)
over a series of measurements, leaving the error close to the
level set by equipment tolerances, propagation effects, and so
Figure E13 Tracking error with strong specular reflection (from forth. DKB, SAL
Barton, 1988, p. 524). Ref.: Barton (1969), (1988), pp. 401–404; Leonov (1988), p. 27.
Peak error is the magnitude of the largest error in radar data,
Errors in azimuth and range coordinates will also be pro-
generally two to three times the rms error.
duced, but these are usually of lesser importance than the ele-
vation error. DKB Peak-to-peak error is the difference between the largest pos-
Ref.: Barton (1988), pp. 512–531. itive and negative errors in radar data, generally four to six
times the rms error.
Noise error is an error caused by noise (generally of thermal
origin) entering the radar receiver. This error component