Page 76 - Radiochemistry and nuclear chemistry

Unstable Nuclei and Radioactive Decay 65

The spin attributed to the neutrino allows conservation of angular momentum; in our
example, the total spin of the products would be 11/2 + 1/2 + 1/2 or 13/2, and when the
spin of 137Cs, 7/2, is subtracted from this the result is 6/2 which is an acceptable integral
value. Thus the decay reaction above is incomplete and must be written

137Cs ~ 137mBa +/3- + i,

Notice we have replaced J, by ~, which is the designation of the antineutrino. Beta-decay
theory has shown that antineutrinos ~ are emitted in electron decay, and "regular" neutrinos
p in positron decay. We can consider the particles identical; cf. w Because of the
extremely low probability of interaction or neutrinos with matter, they are unfortunately
often omitted in writing B-decay reactions.
The neutrino theory also explains the energy spectrum in /3-decay. However, this
necessitates the introduction of another important nuclear concept, that of relativistic mass
and rest mass. In 1901 S. G. Kaufmann showed in experiments that the mass of an electron
m seemed to increase when its velocity v approached that of the speed of light c. It was
found that this increase followed an expression

m = m ~ (1 - v2/c 2)-~ (4.19)

based on H. Lorentz's studies of the relation between distance, speed of light, and time.
m ~ is the rest mass of the particle (at velocity v = 0), while m is referred to as the
relativistic mass. This relation is valid for any moving object, macroscopic or microscopic,
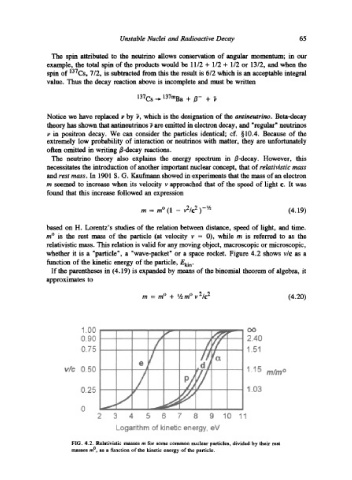
whether it is a "particle', a "wave-packet" or a space rocket. Figure 4.2 shows v/c as a
function of the kinetic energy of the particle, Eki n.
If the parentheses in (4.19) is expanded by means of the binomial theorem of algebra, it
approximates to

m = m ~ + '/2 m~ 2/c2 (4.20)

FIG. 4.2. Relativistic masses m for some common nuclear particles, divided by their rest
masses m ~ as a function of the kinetic energy of the particle.