Page 50 - Rapid Learning in Robotics

36 Artificial Neural Networks

X X

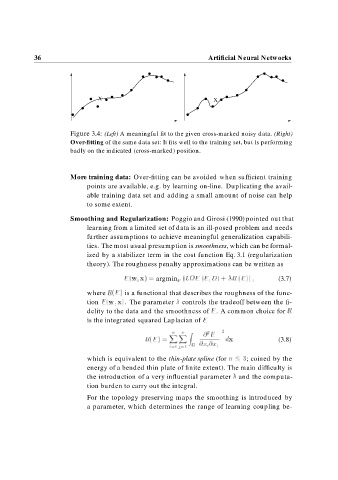
Figure 3.4: (Left) A meaningful fit to the given cross-marked noisy data. (Right)
Over-fitting of the same data set: It fits well to the training set, but is performing
badly on the indicated (cross-marked) position.

More training data: Over-fitting can be avoided when sufficient training
points are available, e.g. by learning on-line. Duplicating the avail-
able training data set and adding a small amount of noise can help
to some extent.

Smoothing and Regularization: Poggio and Girosi (1990) pointed out that
learning from a limited set of data is an ill-posed problem and needs
further assumptions to achieve meaningful generalization capabili-
ties. The most usual presumption is smoothness, which can be formal-
ized by a stabilizer term in the cost function Eq. 3.1 (regularization
theory). The roughness penalty approximations can be written as

F w x argmin LOF F D R F (3.7)
F

where R F is a functional that describes the roughness of the func-
tion F w x . The parameter controls the tradeoff between the fi-
delity to the data and the smoothness of F. A common choice for R
is the integrated squared Laplacian of F
n n Z

F
X X
R F dx (3.8)

i j D
i x
j x

which is equivalent to the thin-plate spline (for n ; coined by the
energy of a bended thin plate of finite extent). The main difficulty is
the introduction of a very influential parameter and the computa-
tion burden to carry out the integral.
For the topology preserving maps the smoothing is introduced by
a parameter, which determines the range of learning coupling be-