Page 53 -

38 CHAPTER 2 Experimental research

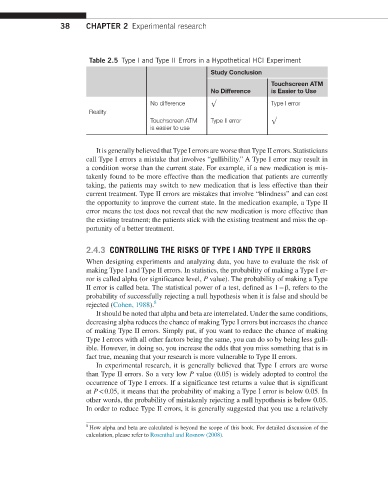
Table 2.5 Type I and Type II Errors in a Hypothetical HCI Experiment
Study Conclusion
Touchscreen ATM
No Difference is Easier to Use
No difference √ Type I error
Reality
Touchscreen ATM Type II error √
is easier to use

It is generally believed that Type I errors are worse than Type II errors. Statisticians
call Type I errors a mistake that involves “gullibility.” A Type I error may result in
a condition worse than the current state. For example, if a new medication is mis-
takenly found to be more effective than the medication that patients are currently
taking, the patients may switch to new medication that is less effective than their
current treatment. Type II errors are mistakes that involve “blindness” and can cost
the opportunity to improve the current state. In the medication example, a Type II
error means the test does not reveal that the new medication is more effective than
the existing treatment; the patients stick with the existing treatment and miss the op-
portunity of a better treatment.

2.4.3 CONTROLLING THE RISKS OF TYPE I AND TYPE II ERRORS

When designing experiments and analyzing data, you have to evaluate the risk of
making Type I and Type II errors. In statistics, the probability of making a Type I er-
ror is called alpha (or significance level, P value). The probability of making a Type
II error is called beta. The statistical power of a test, defined as 1 − β, refers to the
probability of successfully rejecting a null hypothesis when it is false and should be
rejected (Cohen, 1988). 8
It should be noted that alpha and beta are interrelated. Under the same conditions,
decreasing alpha reduces the chance of making Type I errors but increases the chance
of making Type II errors. Simply put, if you want to reduce the chance of making
Type I errors with all other factors being the same, you can do so by being less gull-
ible. However, in doing so, you increase the odds that you miss something that is in
fact true, meaning that your research is more vulnerable to Type II errors.
In experimental research, it is generally believed that Type I errors are worse
than Type II errors. So a very low P value (0.05) is widely adopted to control the
occurrence of Type I errors. If a significance test returns a value that is significant
at P < 0.05, it means that the probability of making a Type I error is below 0.05. In
other words, the probability of mistakenly rejecting a null hypothesis is below 0.05.
In order to reduce Type II errors, it is generally suggested that you use a relatively

8
How alpha and beta are calculated is beyond the scope of this book. For detailed discussion of the
calculation, please refer to Rosenthal and Rosnow (2008).