Page 256 - Reservoir Geomechanics

237 Wellbore failure and stress determination in deviated wells

a. b. X (North)
d
y y r
s b
X Y (East)
w s q
3
s x
tmin s 1 s
Y
x
s b f
2
z s
s
rr
Z
q
Rotation Angle Geographic Stress
a
s b
tmax
z
g Z (Down) b
c. d.
s tmax
1.0
0.5
s
q tf1 tmin q tf2
s rr
0
0 30 60 90 120 150 180
q, degree

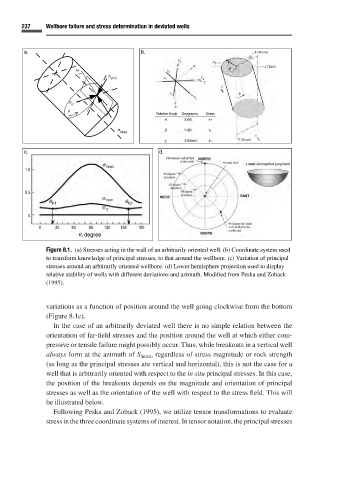
Figure 8.1. (a) Stresses acting in the wall of an arbitrarily oriented well. (b) Coordinate system used
to transform knowledge of principal stresses, to that around the wellbore. (c) Variation of principal
stresses around an arbitrarily oriented wellbore. (d) Lower hemisphere projection used to display
relative stability of wells with different deviations and azimuth. Modified from Peska and Zoback
(1995).

variations as a function of position around the well going clockwise from the bottom
(Figure 8.1c).
In the case of an arbitrarily deviated well there is no simple relation between the
orientation of far-field stresses and the position around the well at which either com-
pressive or tensile failure might possibly occur. Thus, while breakouts in a vertical well
always form at the azimuth of S hmin ,regardless of stress magnitude or rock strength
(as long as the principal stresses are vertical and horizontal), this is not the case for a
well that is arbitrarily oriented with respect to the in situ principal stresses. In this case,
the position of the breakouts depends on the magnitude and orientation of principal
stresses as well as the orientation of the well with respect to the stress field. This will
be illustrated below.
Following Peska and Zoback (1995), we utilize tensor transformations to evaluate
stress in the three coordinate systems of interest. In tensor notation, the principal stresses