Page 91 - Reservoir Geomechanics

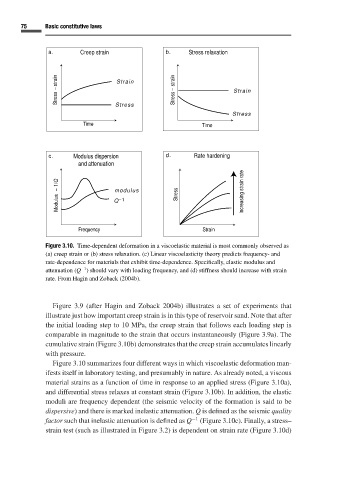
75 Basic constitutive laws

a. Creep strain b. Stress relaxation

Stress - strain Strain Stress - strain Strain

Stress
Stress
Time Time

c. Modulus dispersion d. Rate hardening
and attenuation

Modulus - 1/Q Q −1 Stress Increasing strain rate
modulus

Frequency Strain

Figure 3.10. Time-dependent deformation in a viscoelastic material is most commonly observed as
(a) creep strain or (b) stress relaxation. (c) Linear viscoelasticity theory predicts frequency- and
rate-dependence for materials that exhibit time-dependence. Specifically, elastic modulus and
−1
attenuation (Q ) should vary with loading frequency, and (d) stiffness should increase with strain
rate. From Hagin and Zoback (2004b).

Figure 3.9 (after Hagin and Zoback 2004b) illustrates a set of experiments that
illustrate just how important creep strain is in this type of reservoir sand. Note that after
the initial loading step to 10 MPa, the creep strain that follows each loading step is
comparable in magnitude to the strain that occurs instantaneously (Figure 3.9a). The
cumulative strain (Figure 3.10b) demonstrates that the creep strain accumulates linearly
with pressure.
Figure 3.10 summarizes four different ways in which viscoelastic deformation man-
ifests itself in laboratory testing, and presumably in nature. As already noted, a viscous
material strains as a function of time in response to an applied stress (Figure 3.10a),
and differential stress relaxes at constant strain (Figure 3.10b). In addition, the elastic
moduli are frequency dependent (the seismic velocity of the formation is said to be
dispersive) and there is marked inelastic attenuation. Q is defined as the seismic quality
factor such that inelastic attenuation is defined as Q −1 (Figure 3.10c). Finally, a stress–
strain test (such as illustrated in Figure 3.2)is dependent on strain rate (Figure 3.10d)