Page 74 -

2.6 Stability Theory 55

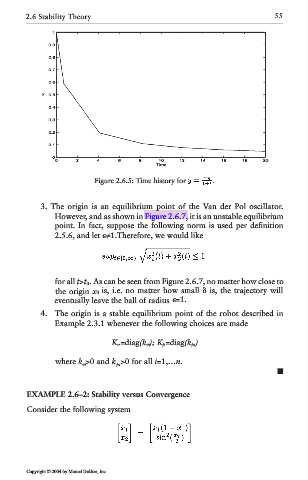
Figure 2.6.5: Time history for

3. The origin is an equilibrium point of the Van der Pol oscillator.
However, and as shown in Figure 2.6.7, it is an unstable equilibrium
point. In fact, suppose the following norm is used per definition
2.5.6, and let ≠1.Therefore, we would like

for all t>t 0 . As can be seen from Figure 2.6.7, no matter how close to
the origin x 0 is, i.e. no matter how small is, the trajectory will
eventually leave the ball of radius =1.
4. The origin is a stable equilibrium point of the robot described in
Example 2.3.1 whenever the following choices are made

K v =diag(k vi ); K p =diag(k pi )

where k vi >0 and k pi >0 for all i=1,…n.

EXAMPLE 2.6–2: Stability versus Convergence
Consider the following system

Copyright © 2004 by Marcel Dekker, Inc.