Page 81 -

62 Introduction to Control Theory

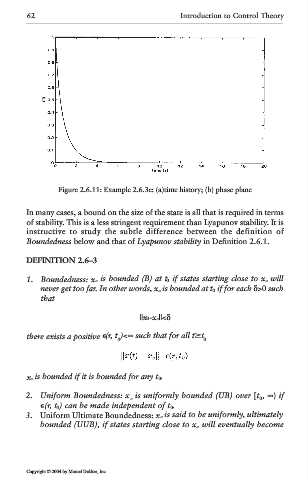
Figure 2.6.11: Example 2.6.3e: (a)time history; (b) phase plane

In many cases, a bound on the size of the state is all that is required in terms
of stability. This is a less stringent requirement than Lyapunov stability. It is
instructive to study the subtle difference between the definition of
Boundedness below and that of Lyapunov stability in Definition 2.6.1.

DEFINITION 2.6–3

1. Boundedness: x e is bounded (B) at t 0 if states starting close to x e will
never get too far. In other words, x e is bounded at t 0 if for each δ>0 such
that
||x 0-x e||<δ

there exists a positive (r, t )<∞ such that for all t t
0 0

x e is bounded if it is bounded for any t 0.

2. Uniform Boundedness: x e is uniformly bounded (UB) over [t 0, ∞) if
(r, t 0) can be made independent of t 0.
3. Uniform Ultimate Boundedness: x e is said to be uniformly, ultimately
bounded (UUB), if states starting close to x e will eventually become

Copyright © 2004 by Marcel Dekker, Inc.