Page 149 - Rock Mechanics For Underground Mining

MODELS OF DISCONTINUITY STRENGTH AND DEFORMATION

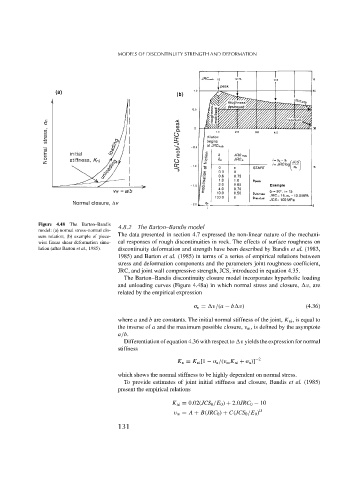
Figure 4.48 The Barton–Bandis 4.8.2 The Barton–Bandis model
model: (a) normal stress–normal clo-
sure relation; (b) example of piece- The data presented in section 4.7 expressed the non-linear nature of the mechani-
wise linear shear deformation simu- cal responses of rough discontinuities in rock. The effects of surface roughness on
lation (after Barton et al., 1985). discontinuity deformation and strength have been described by Bandis et al. (1983,
1985) and Barton et al. (1985) in terms of a series of empirical relations between
stress and deformation components and the parameters joint roughness coefficient,
JRC, and joint wall compressive strength, JCS, introduced in equation 4.35.
The Barton–Bandis discontinuity closure model incorporates hyperbolic loading
and unloading curves (Figure 4.48a) in which normal stress and closure, v, are
related by the empirical expression

n = v/(a − b v) (4.36)

where a and b are constants. The initial normal stiffness of the joint, K ni , is equal to
the inverse of a and the maximum possible closure, v m , is defined by the asymptote
a/b.
Differentiation of equation 4.36 with respect to v yields the expression for normal
stiffness
K n = K ni [1 − n /(v m K ni + n )] −2

which shows the normal stiffness to be highly dependent on normal stress.
To provide estimates of joint initial stiffness and closure, Bandis et al. (1985)
present the empirical relations

K ni = 0.02(JCS 0 /E 0 ) + 2.0JRC 0 − 10
v m = A + B(JRC 0 ) + C(JCS 0 /E 0 ) D
131