Page 321 - Rock Mechanics For Underground Mining

INSTABILITY DUE TO FAULT SLIP

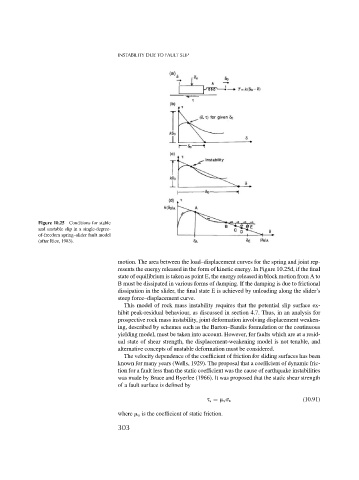
Figure 10.25 Conditions for stable
and unstable slip in a single-degree-
of-freedom spring–slider fault model
(after Rice, 1983).

motion. The area between the load–displacement curves for the spring and joint rep-
resents the energy released in the form of kinetic energy. In Figure 10.25d, if the final
state of equilibrium is taken as point E, the energy released in block motion from A to
B must be dissipated in various forms of damping. If the damping is due to frictional
dissipation in the slider, the final state E is achieved by unloading along the slider’s
steep force–displacement curve.
This model of rock mass instability requires that the potential slip surface ex-
hibit peak-residual behaviour, as discussed in section 4.7. Thus, in an analysis for
prospective rock mass instability, joint deformation involving displacement weaken-
ing, described by schemes such as the Barton–Bandis formulation or the continuous
yielding model, must be taken into account. However, for faults which are at a resid-
ual state of shear strength, the displacement-weakening model is not tenable, and
alternative concepts of unstable deformation must be considered.
The velocity dependence of the coefficient of friction for sliding surfaces has been
known for many years (Wells, 1929). The proposal that a coefficient of dynamic fric-
tion for a fault less than the static coefficient was the cause of earthquake instabilities
was made by Brace and Byerlee (1966). It was proposed that the static shear strength
of a fault surface is defined by

(10.91)
s =
s n
where
s is the coefficient of static friction.

303