Page 320 - Rock Mechanics For Underground Mining

ENERGY, MINE STABILITY, MINE SEISMICITY AND ROCKBURSTS

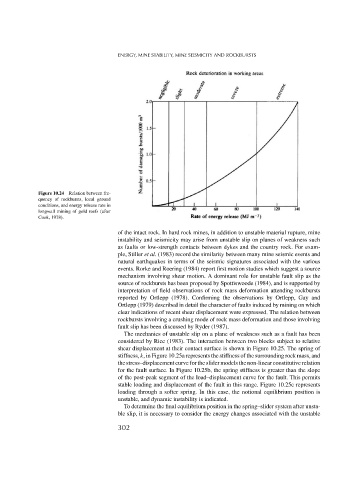
Figure 10.24 Relation between fre-
quency of rockbursts, local ground
conditions, and energy release rate in
longwall mining of gold reefs (after
Cook, 1978).

of the intact rock. In hard rock mines, in addition to unstable material rupture, mine
instability and seismicity may arise from unstable slip on planes of weakness such
as faults or low-strength contacts between dykes and the country rock. For exam-
ple, Stiller et al. (1983) record the similarity between many mine seismic events and
natural earthquakes in terms of the seismic signatures associated with the various
events. Rorke and Roering (1984) report first motion studies which suggest a source
mechanism involving shear motion. A dominant role for unstable fault slip as the
source of rockbursts has been proposed by Spottiswoode (1984), and is supported by
interpretation of field observations of rock mass deformation attending rockbursts
reported by Ortlepp (1978). Confirming the observations by Ortlepp, Gay and
Ortlepp (1979) described in detail the character of faults induced by mining on which
clear indications of recent shear displacement were expressed. The relation between
rockbursts involving a crushing mode of rock mass deformation and those involving
fault slip has been discussed by Ryder (1987).
The mechanics of unstable slip on a plane of weakness such as a fault has been
considered by Rice (1983). The interaction between two blocks subject to relative
shear displacement at their contact surface is shown in Figure 10.25. The spring of
stiffness, k, in Figure 10.25a represents the stiffness of the surrounding rock mass, and
the stress–displacement curve for the slider models the non-linear constitutive relation
for the fault surface. In Figure 10.25b, the spring stiffness is greater than the slope
of the post-peak segment of the load–displacement curve for the fault. This permits
stable loading and displacement of the fault in this range. Figure 10.25c represents
loading through a softer spring. In this case, the notional equilibrium position is
unstable, and dynamic instability is indicated.
To determine the final equilibrium position in the spring–slider system after unsta-
ble slip, it is necessary to consider the energy changes associated with the unstable

302