Page 63 - Rock Mechanics For Underground Mining
P. 63
PROBLEMS
where C 1 , C 2 are indefinite constants.
(a) Establish expressions for the normal and shear strain components, ε xx , ε yy , xy .
(b) Verify that the expressions for the strains satisfy the strain compatibility equa-
tions.
(c) Using the stress–strain relations for isotropic elasticity, establish expressions for
the stress components induced by the loading system.
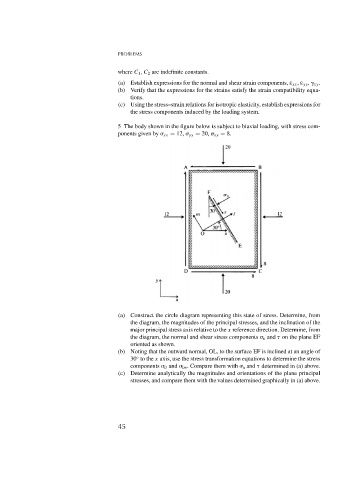
5 The body shown in the figure below is subject to biaxial loading, with stress com-
ponents given by xx = 12, yy = 20, xy = 8.
(a) Construct the circle diagram representing this state of stress. Determine, from
the diagram, the magnitudes of the principal stresses, and the inclination of the
major principal stress axis relative to the x reference direction. Determine, from
the diagram, the normal and shear stress components n and on the plane EF
oriented as shown.
(b) Noting that the outward normal, OL, to the surface EF is inclined at an angle of
30 to the x axis, use the stress transformation equations to determine the stress
◦
components ll and lm . Compare them with n and determined in (a) above.
(c) Determine analytically the magnitudes and orientations of the plane principal
stresses, and compare them with the values determined graphically in (a) above.
45