Page 379 - Schaum's Outline of Differential Equations

362 ANSWERS TO SUPPLEMENTARY PROBLEMS

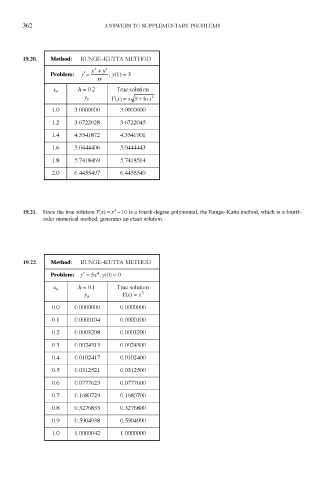
19.20. Method: RUNGE-KUTTA METHOD

Proble

h = 0.2 True solution
x n
y n Y(x) = x^9 + \nx 2
1.0 3.0000000 3.0000000

1.2 3.6722028 3.6722045
1.4 4.3541872 4.3541901

1.6 5.0444406 5.0444443
1.8 5.7418469 5.7418514

2.0 6.4455497 6.4455549

4
19.21. Since the true solution Y(x) =x - 10 is a fourth-degree polynomial, the Runge-Kutta method, which is a fourth-
order numerical method, generates an exact solution.

19.22. Method: RUNGE-KUTTA METHOD

4
Problem: / = 5x ; y(0) = 0
ft = 0.1 True solution
x n 5
y n Y(x) = x
0.0 0.0000000 0.0000000

0.1 0.0000104 0.0000100
0.2 0.0003208 0.0003200

0.3 0.0024313 0.0024300
0.4 0.0102417 0.0102400

0.5 0.0312521 0.0312500
0.6 0.0777625 0.0777600

0.7 0.1680729 0.1680700
0.8 0.3276833 0.3276800

0.9 0.5904938 0.5904900
1.0 1.0000042 1.0000000