Page 384 - Schaum's Outline of Differential Equations

ANSWERS TO SUPPLEMENTARY PROBLEMS 367

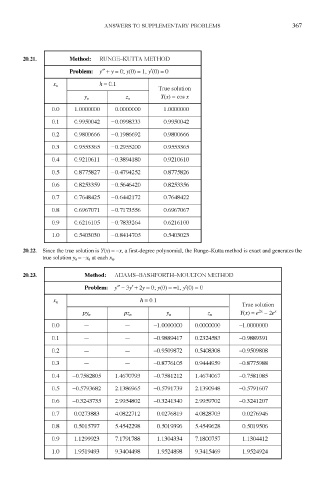
20.21. Method: RUNGE-KUTTA METHOD

Problem: /' + y = 0; y(0) = 1 , /(O) = 0
ft = 0.1
x n
True solution
y n •^n Y(x) = cos x
•7
0.0 1.0000000 0.0000000 1.0000000

0.1 0.9950042 -0.0998333 0.9950042
0.2 0.9800666 -0.1986692 0.9800666

0.3 0.9553365 -0.2955200 0.9553365
0.4 0.9210611 -0.3894180 0.9210610

0.5 0.8775827 -0.4794252 0.8775826
0.6 0.8253359 -0.5646420 0.8253356

0.7 0.7648425 -0.6442172 0.7648422
0.8 0.6967071 -0.7173556 0.6967067

0.9 0.6216105 -0.7833264 0.6216100
1.0 0.5403030 -0.8414705 0.5403023

20.22. Since the true solution is Y(x) = -x, a first-degree polynomial, the Runge-Kutta method is exact and generates the
true solutiionyn=-xm ateachxn

20.23. Method: ADAMS-BASHFORTH-MOULTON METHOD

Problem: y" - 3y' + 2y = 0; y(0) = -1 , /(O) = 0
h = 0.l
x n
True solution
py n PZ n y n •^n Y(x) = e - 2e x
2x
•7
0.0 — — -1.0000000 0.0000000 -1.0000000
0.1 — — -0.9889417 0.2324583 -0.9889391
0.2 — — -0.9509872 0.5408308 -0.9509808

0.3 — — -0.8776105 0.9444959 -0.8775988
0.4 -0.7582805 1.4670793 -0.7581212 1.4674067 -0.7581085

0.5 -0.5793682 2.1386965 -0.5791739 2.1390948 -0.5791607
0.6 -0.3243735 2.9954802 -0.3241340 2.9959702 -0.3241207

0.7 0.0273883 4.0822712 0.0276819 4.0828703 0.0276946
0.8 0.5015797 5.4542298 0.5019396 5.4549628 0.5019506

0.9 1.1299923 7.1791788 1.1304334 7.1800757 1.1304412
1.0 1.9519493 9.3404498 1.9524898 9.3415469 1.9524924