Page 102 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 5] INTEGRALS 93

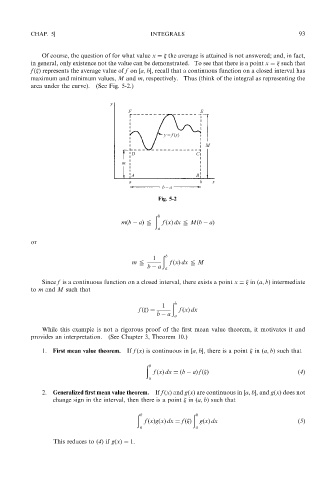
Of course, the question of for what value x ¼ the average is attained is not answered; and, in fact,
in general, only existence not the value can be demonstrated. To see that there is a point x ¼ such that
f ð Þ represents the average value of f on ½a; bŠ, recall that a continuous function on a closed interval has
maximum and minimum values, M and m, respectively. Thus (think of the integral as representing the
area under the curve). (See Fig. 5-2.)

y
F E

y = f (x)
M
D C
m
A B
a b x
_
b a
Fig. 5-2

b
ð
mðb aÞ @ f ðxÞ dx @ Mðb aÞ
a
or

1 ð b
m @ f ðxÞ dx @ M
b a a
Since f is a continuous function on a closed interval, there exists a point x ¼ in ða; bÞ intermediate
to m and M such that

1 ð b
f ðxÞ dx
f ð Þ¼
b a a
While this example is not a rigorous proof of the first mean value theorem, it motivates it and
provides an interpretation. (See Chapter 3, Theorem 10.)

1. First mean value theorem. If f ðxÞ is continuous in ½a; bŠ, there is a point in ða; bÞ such that

ð b
f ðxÞ dx ¼ðb aÞ f ð Þ ð4Þ
a
2. Generalized first mean value theorem. If f ðxÞ and gðxÞ are continuous in ½a; bŠ,and gðxÞ does not
change sign in the interval, then there is a point in ða; bÞ such that

b b
ð ð
gðxÞ dx
f ðxÞgðxÞ dx ¼ f ð Þ ð5Þ
a a
This reduces to (4)if gðxÞ¼ 1.