Page 130 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 6] PARTIAL DERIVATIVES 121

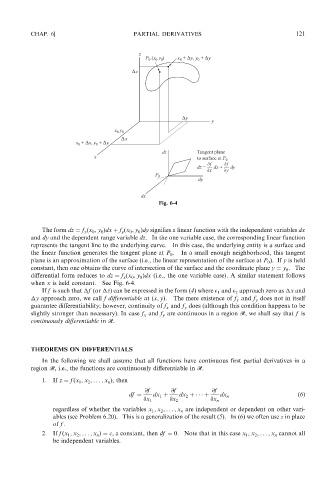
Fig. 6-4

The form dz ¼ f x ðx 0 ; y 0 Þdx þ f y ðx 0 ; y 0 Þdy signifies a linear function with the independent variables dx
and dy and the dependent range variable dz.In the one variable case, the corresponding linear function
represents the tangent line to the underlying curve. In this case, the underlying entity is a surface and
the linear function generates the tangent plane at P 0 . Ina small enough neighborhood, this tangent
plane is an approximation of the surface (i.e., the linear representation of the surface at P 0 ). If y is held
constant, then one obtains the curve of intersection of the surface and the coordinate plane y ¼ y 0 . The
differential form reduces to dz ¼ f x ðx 0 ; y 0 Þdx (i.e., the one variable case). A similar statement follows
when x is held constant. See Fig. 6-4.
If f is such that f (or zÞ can be expressed in the form (4) where 1 and 2 approach zero as x and
y approach zero, we call f differentiable at ðx; yÞ. The mere existence of f x and f y does not in itself
guarantee differentiability; however, continuity of f x and f y does (although this condition happens to be
slightly stronger than necessary). In case f x and f y are continuous in a region r,we shall say that f is
continuously differentiable in r.

THEOREMS ON DIFFERENTIALS
In the following we shall assume that all functions have continuous first partial derivatives in a
region r, i.e., the functions are continuously differentiable in r.
1. If z ¼ f ðx 1 ; x 2 ; ... ; x n Þ, then
@f @f @f
dx n
df ¼ dx 1 þ dx 2 þ þ ð6Þ
@x 1 @x 2 @x n
regardless of whether the variables x 1 ; x 2 ; ... ; x n are independent or dependent on other vari-
ables (see Problem 6.20). This is a generalization of the result (5). In (6)we often use z in place
of f .
2. If f ðx 1 ; x 2 ; ... ; x n Þ¼ c,a constant, then df ¼ 0. Note that in this case x 1 ; x 2 ; ... ; x n cannot all
be independent variables.