Page 166 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 7] VECTORS 157

dA dA 1 dA 2 dA 3
k
du du du du
¼
j þ
i þ
2
2
Higher derivatives such as d A=du , etc., can be similarly defined.
3. If Aðx; y; zÞ¼ A 1 ðx; y; zÞi þ A 2 ðx; y; zÞj þ A 3 ðx; y; zÞk, then
@A @A @A
dz
dA ¼ dx þ dy þ
@x @y @z
is the differential of A.
4. Derivatives of products obey rules similar to those for scalar functions. However, when cross
products are involved the order may be important. Some examples are
d dA d
¼ A;
ðaÞ ð AÞ þ
du du du
@ @B @A
B;
ðbÞ ðA BÞ¼ A þ
@y @y @y
@ @B @A
B
ðcÞ ðA BÞ¼ A þ (Maintain the order of A and BÞ
@z @z @z
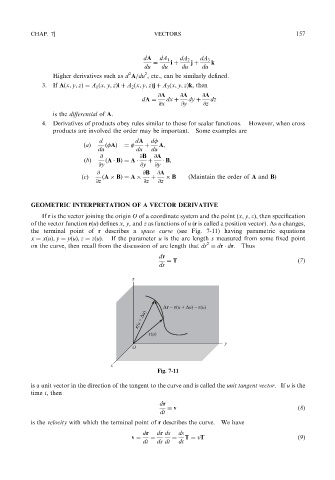
GEOMETRIC INTERPRETATION OF A VECTOR DERIVATIVE
If r is the vector joining the origin O of a coordinate system and the point ðx; y; zÞ, then specification
of the vector function rðuÞ defines x, y; and z as functions of u (r is called a position vector). As u changes,
the terminal point of r describes a space curve (see Fig. 7-11) having parametric equations
x ¼ xðuÞ; y ¼ yðuÞ; z ¼ zðuÞ. If the parameter u is the arc length s measured from some fixed point
2
on the curve, then recall from the discussion of arc length that ds ¼ dr dr. Thus
dr
¼ T
ds ð7Þ

Fig. 7-11
is a unit vector in the direction of the tangent to the curve and is called the unit tangent vector.If u is the
time t, then
dr
¼ v
dt ð8Þ
is the velocity with which the terminal point of r describes the curve. We have
dr dr ds ds
T ¼ vT
v ¼ ¼ ¼ ð9Þ
dt ds dt dt