Page 290 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 11] INFINITE SERIES 281

ð M
If lim f ðxÞ dx exists and is equal to S,we see from the left-hand inequality in (1)that
M!1 1
u 2 þ u 3 þ þ u M is monotonic increasing and bounded above by S,sothat u n converges.
M
ð
If lim f ðxÞ dx is unbounded, we see from the right-hand inequality in (1)that u n diverges.
M!1 1
Thus the proof is complete.
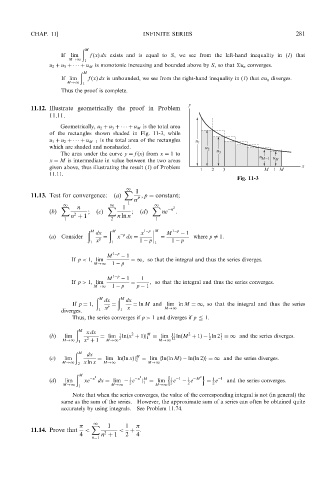
11.12. Illustrate geometrically the proof in Problem
11.11.
Geometrically, u 2 þ u 3 þ þ u M is the total area
of the rectangles shown shaded in Fig. 11-3, while
u 1 þ u 2 þ þ u M 1 is the total area of the rectangles
which are shaded and nonshaded.
The area under the curve y ¼ f ðxÞ from x ¼ 1to
x ¼ M is intermediate in value between the two areas
given above, thus illustrating the result (1)ofProblem
11.11.
Fig. 11-3
1
X 1
11.13. Test for convergence: (a) ; p ¼ constant;
n P
1
1 1 1
X n X 1 X n 2
; ; ne .
ðbÞ 2 ðcÞ ðdÞ
n þ 1 n ln n
1 2 1
ð M dx ð M x 1 p M M 1 p 1
Consider x p where p 6¼ 1:
1 x 1 1 p 1 1 p
ðaÞ p ¼ dx ¼ ¼
M 1 p 1
If p < 1; lim ¼1,sothat the integral and thus the series diverges.
1 p
M!1
M 1 p 1 1
If p > 1; lim ¼ ,sothat the integral and thus the series converges.
1 p p 1
M!1
ð M dx ð M dx
If p ¼ 1, p ¼ ¼ ln M and lim ln M ¼1,sothat the integral and thus the series
diverges. 1 x 1 x M!1
Thus, the series converges if p > 1 and diverges if p @ 1.
ð M xdx
M
2
1
2

lim ¼ lim 1 lnðx þ 1Þj 1 ¼ lim 1 lnðM þ 1Þ ln 2 ¼1 and the series diverges.
1 x þ 1
ðbÞ 2 2 2 2
M!1 M!1 M!1
M dx
ð
M
lim ¼ lim lnðln xÞj 2 ¼ lim flnðln MÞ lnðln 2Þg ¼ 1 and the series diverges.
2 x ln x
ðcÞ
M!1 M!1 M!1
ð M n o
1 M
1 x M
1 1
lim xe x 2 dx ¼ lim e 2 j 1 ¼ lim 1 1 e 2 ¼ e and the series converges.
e
2 2 2 2
ðdÞ
M!1 1 M!1 M!1
Note that when the series converges, the value of the corresponding integral is not (in general) the
same as the sum of the series. However, the approximate sum of a series can often be obtained quite
accurately by using integrals. See Problem 11.74.
X 1 1
1
11.14. Prove that < < þ .
2
4 n þ 1 2 4
n¼1