Page 367 - Schaum's Outline of Theory and Problems of Applied Physics

352 ALTERNATING-CURRENT CIRCUITS [CHAP. 29

L (in henries) when the frequency of the current is f (in hertz) is
Inductive reactance = X L = 2π f L

When a potential difference V of frequency f is applied across an inductor whose reactance is X L at frequency
f , current I = V/X L will flow. The unit of X L is the ohm.
The capacitive reactance of a capacitor is similarly a measure of its effectiveness in resisting the flow of an
alternating current, in this case by virtue of the reverse potential difference across it owing to the accumulation
of charge on its plates. No power loss is associated with a capacitor in an ac circuit. The capacitive reactance X C
of a capacitor whose capacitance is C (in farads) when the frequency of the current is f (in hertz) is

1
Capacitive reactance = X C =
2π f C
When a potential difference of frequency f is applied across a capacitor whose reactance is X C at frequency f ,
current I = V/X C will flow. The unit of X C is the ohm. Evidently reactance takes the place of resistance in
Ohm’s law for finding the ac current in an inductor or a capacitor.

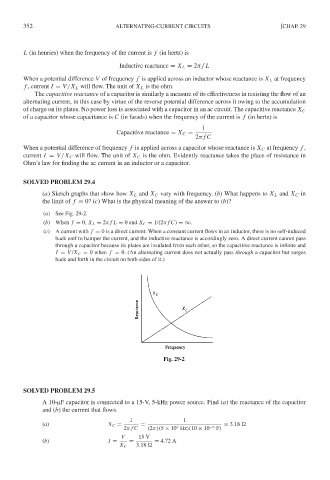
SOLVED PROBLEM 29.4
(a) Sketch graphs that show how X L and X C vary with frequency. (b) What happens to X L and X C in
the limit of f = 0? (c) What is the physical meaning of the answer to (b)?
(a) See Fig. 29-2.
(b) When f = 0, X L = 2π f L = 0 and X C = 1/(2π f C) =∞.
(c) A current with f = 0 is a direct current. When a constant current flows in an inductor, there is no self-induced
back emf to hamper the current, and the inductive reactance is accordingly zero. A direct current cannot pass
through a capacitor because its plates are insulated from each other, so the capacitive reactance is infinite and
I = V /X C = 0 when f = 0. (An alternating current does not actually pass through a capacitor but surges
back and forth in the circuit on both sides of it.)

Fig. 29-2

SOLVED PROBLEM 29.5
A 10-µF capacitor is connected to a 15-V, 5-kHz power source. Find (a) the reactance of the capacitor
and (b) the current that flows.
1 1
(a) X C = = = 3.18
3
2π f C (2π)(5 × 10 Hz)(10 × 10 −6 F)
V 15 V
(b) I = = = 4.72 A
X C 3.18