Page 21 - Schaum's Outline of Theory and Problems of Signals and Systems

10 SIGNALS AND SYSTEMS [CHAP. 1

is an important example of a complex signal. Using Euler's formula, this signal can be
defined as

= eiUo' = cos o,t + jsin w0t
~(t) (1.33)
Thus, x(t) is a complex signal whose real part is cos mot and imaginary part is sin oot. An
important property of the complex exponential signal x(t) in Eq. (1.32) is that it is
periodic. The fundamental period To of x(t) is given by (Prob. 1.9)

Note that x(t) is periodic for any value of o,.

General Complex Exponential Signals:

Let s = a + jw be a complex number. We define x(t) as
~(t) (1 -35)
= eS' = e("+~")' = e"'(cos ot + j sin wt )
Then signal x(t) in Eq. (1.35) is known as a general complex exponential signal whose real
part eu'cos ot and imaginary part eu'sin wt are exponentially increasing (a > 0) or
decreasing (a < 0) sinusoidal signals (Fig. 1-7).

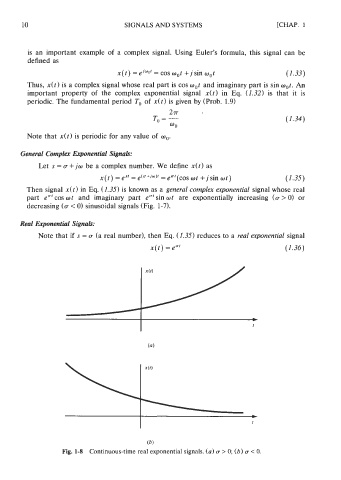
Real Exponential Signals:
Note that if s = a (a real number), then Eq. (1.35) reduces to a real exponential signal

x(t) = em' (1.36)

(b)
Fig. 1-8 Continuous-time real exponential signals. (a) a > 0; (b) a < 0.