Page 26 - Schaum's Outline of Theory and Problems of Signals and Systems

CHAP. 11 SIGNALS AND SYSTEMS 15

Consider the complex exponential sequence with frequency (R, + 27k), where k is an
integer:
ej(ilo+2rrk)n = ejRon j2rrkn - inon
e - e (1 .56)
since ej2"kn = 1. From Eq. (1.56) we see that the complex exponential sequence at
frequency R, is the same as that at frequencies (R, f 27), (R, f 4.~1, and so on.
Therefore, in dealing with discrete-time exponentials, we need only consider an interval of
length 27 in which to choose R,. Usually, we will use the interval 0 I R, < 27 or the
interval - 7 sr R, < 7.

General Complex Exponential Sequences:
The most general complex exponential sequence is often defined as
x[n] = Can (1.57)

where C and a are in general complex numbers. Note that Eq. (1.52) is the special case of
Eq. (1.57) with C = 1 and a = eJRO.

. .
. . . . .
.
I

a 0

-9 -6 6 9
t t b
-I2 1 .3 o 3 1 12 1 n

Ylll '111'

(b)
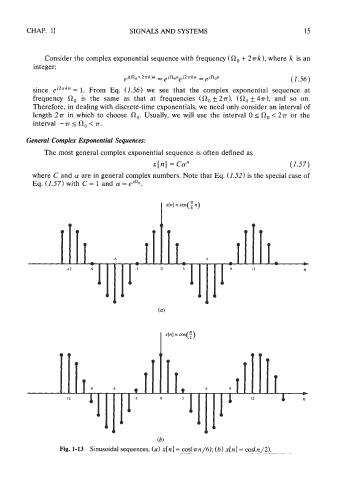
Fig. 1-13 Sinusoidal sequences. (a) x[n] = cos(rrn/6); (b) x[n] = cos(n/2).