Page 343 - Schaum's Outline of Theory and Problems of Signals and Systems

FOURIER ANALYSIS OF DISCRETE-TIME SIGNALS AND SYSTEMS [CHAP. 6

(a) Find the frequency response H(S1) of the system.
(b) Find the impulse response h[n] of the system.
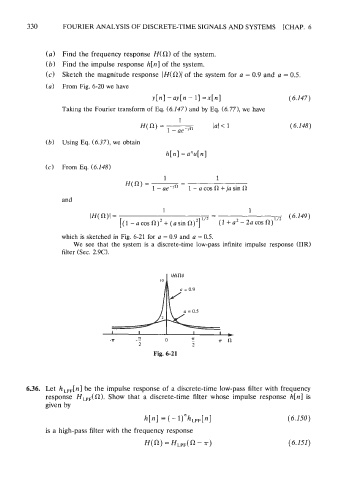
(c) Sketch the magnitude response (H(a)( of the system for a = 0.9 and a = 0.5.

(a) From Fig. 6-20 we have
y[n] - ay[n - 11 =x[n] (6.147)
Taking the Fourier transform of Eq. (6.147) and by Eq. (6.771, we have

(b) Using Eq. (6.371, we obtain
h[n] = anu[n]

(c) From Eq. (6.148)

and

which is sketched in Fig. 6-21 for a = 0.9 and a = 0.5.
We see that the system is a discrete-time low-pass infinite impulse response (IIR)
filter (Sec. 2.90

-
n
-TI - - o T ?r n
2 2
Fig. 6-21

6.36. Let hLpF[n] be the impulse response of a discrete-time 10~4-pass filter with frequency
response HLpF(R). Show that a discrete-time filter whose impulse response h[n] is
given by

h[nl = (- l)"hLPF[nl
is a high-pass filter with the frequency response

H(S1) = HLPF(a T)