Page 418 - Schaum's Outline of Theory and Problems of Signals and Systems
P. 418
CHAP. 71 STATE SPACE ANALYSIS
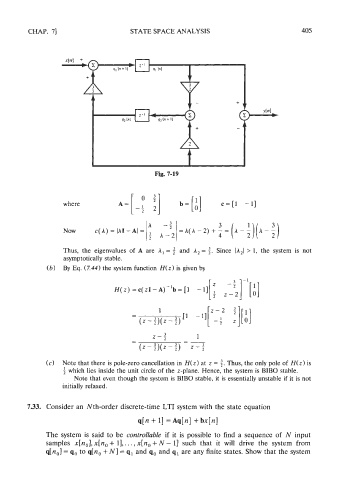
Fig. 7-19
where
Thus, the eigenvalues of A are A, = $ and A, = ;. Since IAzl > 1, the system is not
asymptotically stable.
(b) By Eq. (7.44) the system function H(z) is given by
(c) Note that there is pole-zero cancellation in H(z) at z = :. Thus, the only pole of H(z) is
I
which lies inside the unit circle of the z-plane. Hence, the system is BIBO stable.
Note that even though the system is BIBO stable, it is essentially unstable if it is not
initially relaxed.
7.33. Consider an Nth-order discrete-time LTI system with the state equation
The system is said to be controllable if it is possible to find a sequence of N input
samples x[n,], x[n, + 11, . . . , x[n, f N - 1] such that it will drive the system from
q[n,] = q, to q[n, + N] = q, and q, and q, are any finite states. Show that the system