Page 137 - Schaum's Outlines - Probability, Random Variables And Random Processes

FUNCTIONS OF RANDOM VARIABLES, EXPECTATION, LIMIT THEOREMS [CHAP. 4

and

which indicates that Z = N(0; 1).

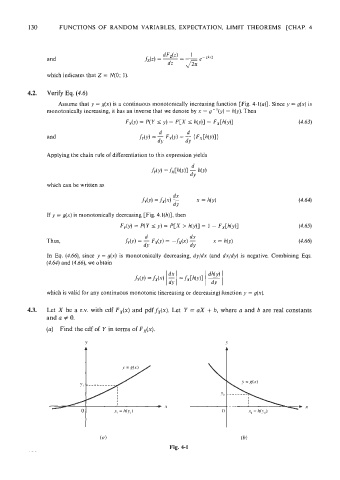
4.2. Verify Eq. (4.6).
Assume that y = g(x) is a continuous monotonically increasing function [Fig. 4-l(a)]. Since y = g(x) is
monotonically increasing, it has an inverse that we denote by x = g-'(y) = h(y). Then

Applying the chain rule of differentiation to this expression yields

which can be written as

If y = g(x) is monotonically decreasing [Fig. 4.l(b)], then
Fdy) = P( Y I y) = P[X > h(y)] = 1 - Fx[h(y)]
d dx
= - FAY) = -fx(x) -
Thus, ~Y(Y) x = h(y) (4.66)
dy dy
In Eq. (4.66), since y = g(x) is monotonically decreasing, dy/dx (and dxldy) is negative. Combining Eqs.
(4.64) and (4.66), we obtain

which is valid for any continuous monotonic (increasing or decreasing) function y = g(x).

4.3. Let X be a r.v. with cdf F,(x) and pdf f,(x). Let Y =. ax + b, where a and b are real constants
and a # 0.
(a) Find the cdf of Y in terms of F,(x).

Fig. 4-1