Page 62 - Schaum's Outlines - Probability, Random Variables And Random Processes

CHAP. 21 RANDOM VARIABLES

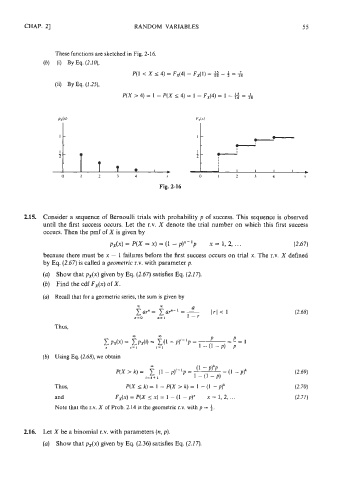
These functions are sketched in Fig. 2-16.
(b) (9 BY Eq. (2.m

P(l < X 1 4) = Fx(4) - Fx(X) = - 3 =
(ii) By Eq. (1 .Z),
P(X > 4) = 1 - P(X 5 4) = 1 - Fx(4) = 1 - = -&

Fig. 2-16

2.15. Consider a sequence of Bernoulli trials with probability p of success. This sequence is observed
until the first success occurs. Let the r.v. X denote the trial number on which this first success
occurs. Then the pmf of X is given by

because there must be x - 1 failures before the first success occurs on trial x. The r.v. X defined
by Eq. (2.67) is called a geometric r.v. with parameter p.
(a) Show that px(x) given by Eq. (2.67) satisfies Eq. (2.1 7).
(b) Find the cdf F,(x) of X.
(a) Recall that for a geometric series, the sum is given by

Thus,

(b) Using Eq. (2.68), we obtain

Thus, P(X 5 k) = 1 - P(X > k) = 1 - (1 -
and Fx(x)=P(X<~)=1-(1-p)" x=1,2, ...
Note that the r.v. X of Prob. 2.14 is the geometric r.v. with p == 4.

2.16. Let X be a binomial r.v. with parameters (n, p).
(a) Show that p&) given by Eq. (2.36) satisfies Eq. (2.1 7).