Page 138 - Semiconductor For Micro- and Nanotechnology An Introduction For Engineers

Periodic Potentials in Crystal
Compare this result with the case of a single potential box given in Sec-
tion 3.2.1. The major difference is that in the periodic case there are
regions of κa where a whole continuum of solutions is possible, whereas
in the single well case we have only discrete values.
Moving The transition between the two situations can be easily seen by making b
Atoms in (3.97) very large. In this way we recover (3.32) from (3.97). This pro-
Together
cedure corresponds to moving atoms away from each other. Another
effect is given by adding to a single well potential a second identical
b
potential box at a distance , then a third one and so on. The case of two
potential boxes at distance gives rise to the question of what happens
b
with the lowest energy levels that each box contributes to the total sys-
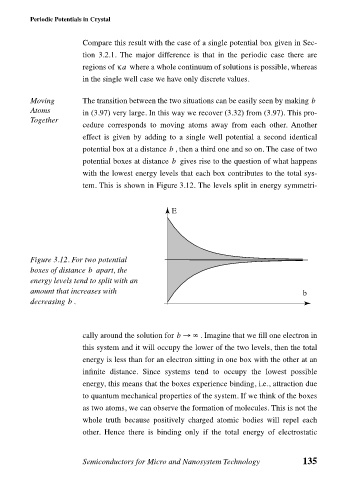
tem. This is shown in Figure 3.12. The levels split in energy symmetri-

E

Figure 3.12. For two potential
b
boxes of distance apart, the
energy levels tend to split with an
amount that increases with b
b
decreasing .

cally around the solution for b → ∞ . Imagine that we fill one electron in
this system and it will occupy the lower of the two levels, then the total
energy is less than for an electron sitting in one box with the other at an
infinite distance. Since systems tend to occupy the lowest possible
energy, this means that the boxes experience binding, i.e., attraction due
to quantum mechanical properties of the system. If we think of the boxes
as two atoms, we can observe the formation of molecules. This is not the
whole truth because positively charged atomic bodies will repel each
other. Hence there is binding only if the total energy of electrostatic

Semiconductors for Micro and Nanosystem Technology 135