Page 181 - Semiconductor For Micro- and Nanotechnology An Introduction For Engineers

Statistics
∏
Q =
i
i
i ∑ exp ( – ( βE + α)n ) (5.22)
n i
i
The product in (5.22) accounts for all states accessible to the system,
while the sum over n depends on how many particles may occupy a
i
state . i
5.2 Particle Statistics: Counting Particles

Different statistical properties of the system arise from the many ways
that the sum in (5.13) and (5.22) has to be performed. Summation over all
i
possible states in turn implies summation over all possible values of
n . We now consider these cases.
i
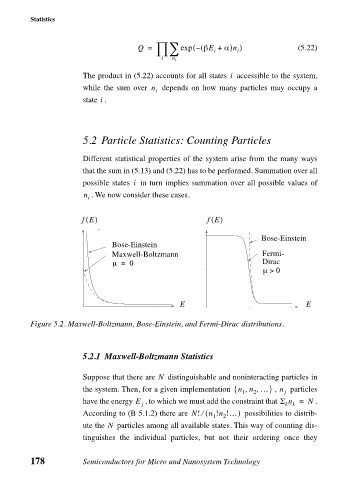
fE() fE()

B
Bose-Einstein
Bose-Einstein
Maxwell-Boltzmann Fermi-
µ = 0 Dirac
µ > 0

E E

Figure 5.2. Maxwell-Boltzmann, Bose-Einstein, and Fermi-Dirac distributions.

5.2.1 Maxwell-Boltzmann Statistics

Suppose that there are N distinguishable and noninteracting particles in
the system. Then, for a given implementation n n …,{ , } , n particles
1 2 j
have the energy E , to which we must add the constraint that Σ n = N .
j k k
According to (B 5.1.2) there are N! (⁄ n !n !…) possibilities to distrib-
1 2
N
ute the particles among all available states. This way of counting dis-
tinguishes the individual particles, but not their ordering once they

178 Semiconductors for Micro and Nanosystem Technology