Page 114 - Structural Steel Designers Handbook AISC, AASHTO, AISI, ASTM, and ASCE-07 Design Standards

Brockenbrough_Ch03.qxd 9/29/05 5:05 PM Page 3.46

CONNECTIONS

3.46 CHAPTER THREE

and then uses virtual work to determine the ultimate
load. The value produced is an upper bound. Therefore,
assuming an incorrect collapse mechanism will produce
unconservative results. The literature contains numerous
examples of yield line analyses for various conditions,
so the correct mechanism is usually easily determined.
Typical cases are discussed in the following. P u repre-
sents the nominal strength for a load applied normal to
the plane of the web and M p is the plastic moment
(M p = 0.25t w F y ). Multiply the nominal strength by φ=
2
0.90 to obtain the design strength.
Web Simply Supported Subjected to an Axial Load.
In general, the web should be assumed as simply sup-
ported when checking the webs of wide flange mem-
bers. If the distance from the top of the connection to the
end of the member is less than u, then dividing the cal-
culated strength by 2 will yield a conservative result.

u = 2 Tab (3.41)
+
ab
+
+ )
)/(
 2[ 2 ( Tab a b + L 2/ ]( a b  )
P = 2 M   (3.42)
u
p
 ab 
If the connection is centered on the web, a = b, then the
equation becomes
−
(
u = TT c) (3.43)
2
 2 T L 
P = 8 M  +  (3.44)
u
p
−
−
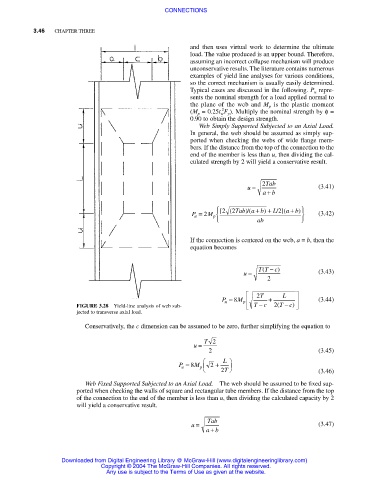
FIGURE 3.28 Yield-line analysis of web sub-  Tc 2( Tc) 
jected to transverse axial load.
Conservatively, the c dimension can be assumed to be zero, further simplifying the equation to
u = T 2
2 (3.45)
 L 
P = 8 M p  2 + 2 T  (3.46)
u
Web Fixed Supported Subjected to an Axial Load. The web should be assumed to be fixed sup-
ported when checking the walls of square and rectangular tube members. If the distance from the top
of the connection to the end of the member is less than u, then dividing the calculated capacity by 2
will yield a conservative result.

u = Tab (3.47)
+
ab

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.