Page 278 - The Combined Finite-Discrete Element Method
P. 278
EXPANSION OF THE DETONATION GAS 261
By substituting the expression for density ρ in terms of specific volume v
1
ρ = (8.13)
v
into equation (8.12), the gas pressure in terms of specific volume is obtained:
b−1 b−1
p c v o 1 + (a/v o )(v o /v c )
= (8.14)
b−1
p o v c 1 + a/v o
As mentioned before, the solution to the expansion of the detonation gas has been obtained
in a closed analytical form.
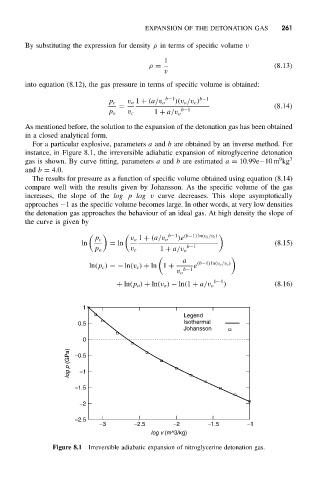
For a particular explosive, parameters a and b are obtained by an inverse method. For
instance, in Figure 8.1, the irreversible adiabatic expansion of nitroglycerine detonation
9
gas is shown. By curve fitting, parameters a and b are estimated a = 10.99e−10 m kg 3
and b = 4.0.
The results for pressure as a function of specific volume obtained using equation (8.14)
compare well with the results given by Johansson. As the specific volume of the gas
increases, the slope of the log p log v curve decreases. This slope asymptotically
approaches −1 as the specific volume becomes large. In other words, at very low densities
the detonation gas approaches the behaviour of an ideal gas. At high density the slope of
the curve is given by
b−1 (b−1) ln(v o /v c )
p c v o 1 + (a/v o )e
ln = ln b−1 (8.15)
p o v c 1 + a/v o
a
ln(p c ) =− ln(v c ) + ln 1 + b−1 e (b−1) ln(v o /v c )
v o
b−1
+ ln(p o ) + ln(v o ) − ln(1 + a/v o ) (8.16)
1
Legend
0.5 Isothermal
Johansson
0
log p (GPa) −0.5
−1
−1.5
−2
−2.5
−3 −2.5 −2 −1.5 −1
log v (m^3/kg)
Figure 8.1 Irreversible adiabatic expansion of nitroglycerine detonation gas.