Page 282 - The Combined Finite-Discrete Element Method

EXPANSION OF THE DETONATION GAS 265

1
0.9
0.8 Isentropic expansion
Pressure change
0.7
+ 10 Pa) 0.6

0.5
p (e 0.4
0.3
0.2
0.1
0
0 0.2 0.4 0.6 0.8 1 1.2 1.4
v (e−02 m^3/kg)
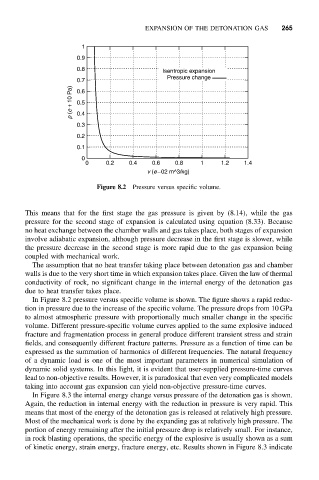
Figure 8.2 Pressure versus specific volume.

This means that for the first stage the gas pressure is given by (8.14), while the gas
pressure for the second stage of expansion is calculated using equation (8.33). Because
no heat exchange between the chamber walls and gas takes place, both stages of expansion
involve adiabatic expansion, although pressure decrease in the first stage is slower, while
the pressure decrease in the second stage is more rapid due to the gas expansion being
coupled with mechanical work.
The assumption that no heat transfer taking place between detonation gas and chamber
walls is due to the very short time in which expansion takes place. Given the law of thermal
conductivity of rock, no significant change in the internal energy of the detonation gas
due to heat transfer takes place.
In Figure 8.2 pressure versus specific volume is shown. The figure shows a rapid reduc-
tion in pressure due to the increase of the specific volume. The pressure drops from 10 GPa
to almost atmospheric pressure with proportionally much smaller change in the specific
volume. Different pressure-specific volume curves applied to the same explosive induced
fracture and fragmentation process in general produce different transient stress and strain
fields, and consequently different fracture patterns. Pressure as a function of time can be
expressed as the summation of harmonics of different frequencies. The natural frequency
of a dynamic load is one of the most important parameters in numerical simulation of
dynamic solid systems. In this light, it is evident that user-supplied pressure-time curves
lead to non-objective results. However, it is paradoxical that even very complicated models
taking into account gas expansion can yield non-objective pressure-time curves.
In Figure 8.3 the internal energy change versus pressure of the detonation gas is shown.
Again, the reduction in internal energy with the reduction in pressure is very rapid. This
means that most of the energy of the detonation gas is released at relatively high pressure.
Most of the mechanical work is done by the expanding gas at relatively high pressure. The
portion of energy remaining after the initial pressure drop is relatively small. For instance,
in rock blasting operations, the specific energy of the explosive is usually shown as a sum
of kinetic energy, strain energy, fracture energy, etc. Results shown in Figure 8.3 indicate