Page 31 - The Combined Finite-Discrete Element Method

14 INTRODUCTION

1
0.9
0.8
0.7
Density 0.6 D = 70.439 mm
D = 59.976 mm
0.5
D = 44.982 mm
0.4 D = 29.988 mm
D = 14.994 mm
0.3 D = 7.497 mm
D = 4.998 mm
0.2 D = 2.635 mm
0.1
0 50 100 150 200 250 300 350
Distance from the bottom (mm)
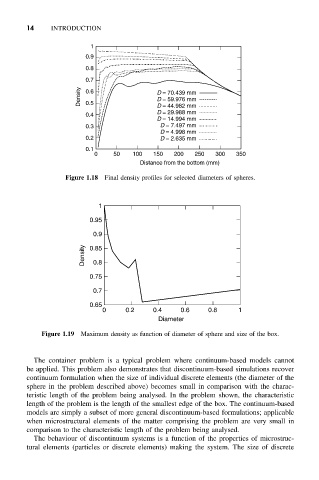
Figure 1.18 Final density profiles for selected diameters of spheres.

1

0.95
0.9
Density 0.85

0.8

0.75
0.7
0.65
0 0.2 0.4 0.6 0.8 1
Diameter
Figure 1.19 Maximum density as function of diameter of sphere and size of the box.

The container problem is a typical problem where continuum-based models cannot
be applied. This problem also demonstrates that discontinuum-based simulations recover
continuum formulation when the size of individual discrete elements (the diameter of the
sphere in the problem described above) becomes small in comparison with the charac-
teristic length of the problem being analysed. In the problem shown, the characteristic
length of the problem is the length of the smallest edge of the box. The continuum-based
models are simply a subset of more general discontinuum-based formulations; applicable
when microstructural elements of the matter comprising the problem are very small in
comparison to the characteristic length of the problem being analysed.
The behaviour of discontinuum systems is a function of the properties of microstruc-
tural elements (particles or discrete elements) making the system. The size of discrete