Page 32 - The Combined Finite-Discrete Element Method

A TYPICAL PROBLEM OF COMPUTATIONAL MECHANICS OF DISCONTINUA 15

elements is not the only parameter governing the behaviour of discontinuum system. This
is demonstrated by using the same container problem as described above. This time size
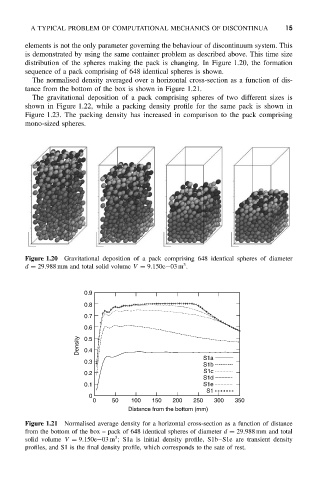
distribution of the spheres making the pack is changing. In Figure 1.20, the formation
sequence of a pack comprising of 648 identical spheres is shown.
The normalised density averaged over a horizontal cross-section as a function of dis-
tance from the bottom of the box is shown in Figure 1.21.
The gravitational deposition of a pack comprising spheres of two different sizes is
shown in Figure 1.22, while a packing density profile for the same pack is shown in
Figure 1.23. The packing density has increased in comparison to the pack comprising
mono-sized spheres.

Figure 1.20 Gravitational deposition of a pack comprising 648 identical spheres of diameter
3
d = 29.988 mm and total solid volume V = 9.150e−03 m .

0.9
0.8
0.7
0.6
Density 0.5
0.4
S1a
0.3
S1b
0.2 S1c
S1d
0.1 S1e
S1
0
0 50 100 150 200 250 300 350
Distance from the bottom (mm)
Figure 1.21 Normalised average density for a horizontal cross-section as a function of distance
from the bottom of the box – pack of 648 identical spheres of diameter d = 29.988 mm and total
3
solid volume V = 9.150e−03 m ; S1a is initial density profile, S1b–S1e are transient density
profiles, and S1 is the final density profile, which corresponds to the sate of rest.