Page 36 - The Combined Finite-Discrete Element Method

A TYPICAL PROBLEM OF COMPUTATIONAL MECHANICS OF DISCONTINUA 19

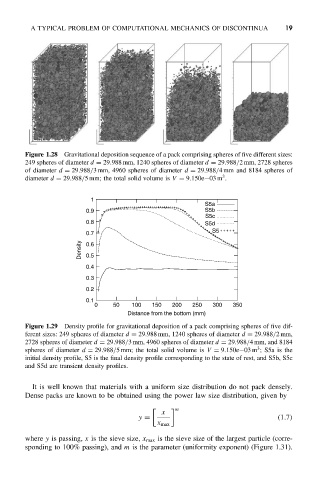
Figure 1.28 Gravitational deposition sequence of a pack comprising spheres of five different sizes:
249 spheres of diameter d = 29.988 mm, 1240 spheres of diameter d = 29.988/2 mm, 2728 spheres
of diameter d = 29.988/3 mm, 4960 spheres of diameter d = 29.988/4 mm and 8184 spheres of
3
diameter d = 29.988/5 mm; the total solid volume is V = 9.150e−03 m .

1
S5a
0.9 S5b
S5c
0.8 S5d
S5
0.7
Density 0.6
0.5
0.4
0.3
0.2
0.1
0 50 100 150 200 250 300 350
Distance from the bottom (mm)
Figure 1.29 Density profile for gravitational deposition of a pack comprising spheres of five dif-
ferent sizes: 249 spheres of diameter d = 29.988 mm, 1240 spheres of diameter d = 29.988/2mm,
2728 spheres of diameter d = 29.988/3 mm, 4960 spheres of diameter d = 29.988/4 mm, and 8184
3
spheres of diameter d = 29.988/5 mm; the total solid volume is V = 9.150e−03 m ; S5a is the
initial density profile, S5 is the final density profile corresponding to the state of rest, and S5b, S5c
and S5d are transient density profiles.

It is well known that materials with a uniform size distribution do not pack densely.
Dense packs are known to be obtained using the power law size distribution, given by
m

x
y = (1.7)
x max
where y is passing, x is the sieve size, x max is the sieve size of the largest particle (corre-
sponding to 100% passing), and m is the parameter (uniformity exponent) (Figure 1.31).