Page 38 - The Combined Finite-Discrete Element Method

A TYPICAL PROBLEM OF COMPUTATIONAL MECHANICS OF DISCONTINUA 21

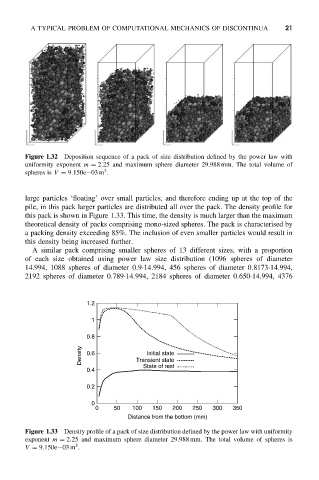
Figure 1.32 Deposition sequence of a pack of size distribution defined by the power law with
uniformity exponent m = 2.25 and maximum sphere diameter 29.988 mm. The total volume of
3
spheres is V = 9.150e−03 m .

large particles ‘floating’ over small particles, and therefore ending up at the top of the
pile, in this pack larger particles are distributed all over the pack. The density profile for
this pack is shown in Figure 1.33. This time, the density is much larger than the maximum
theoretical density of packs comprising mono-sized spheres. The pack is characterised by
a packing density exceeding 85%. The inclusion of even smaller particles would result in
this density being increased further.
A similar pack comprising smaller spheres of 13 different sizes, with a proportion
of each size obtained using power law size distribution (1096 spheres of diameter
14.994, 1088 spheres of diameter 0.9·14.994, 456 spheres of diameter 0.8173·14.994,
2192 spheres of diameter 0.789·14.994, 2184 spheres of diameter 0.650·14.994, 4376

1.2

1

0.8
Density 0.6 Transient state
Initial state

0.4 State of rest

0.2

0
0 50 100 150 200 250 300 350
Distance from the bottom (mm)
Figure 1.33 Density profile of a pack of size distribution defined by the power law with uniformity
exponent m = 2.25 and maximum sphere diameter 29.988 mm. The total volume of spheres is
3
V = 9.150e−03 m .