Page 86 - The Combined Finite-Discrete Element Method
P. 86
ALTERNATIVE IMPLEMENTATION OF THE POTENTIAL CONTACT FORCE 69
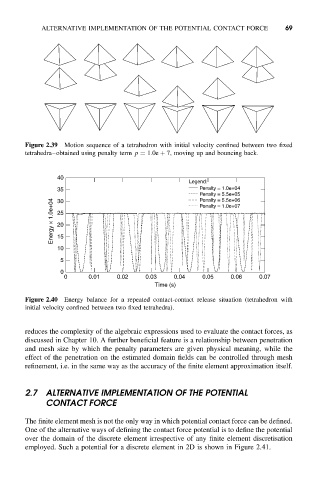
Figure 2.39 Motion sequence of a tetrahedron with initial velocity confined between two fixed
tetrahedra–obtained using penalty term p = 1.0e + 7, moving up and bouncing back.
40
Legend:
35 Penalty = 1.0e+04
Penalty = 5.5e+05
Penalty = 5.5e+06
× 1.0e+04 25 Penalty = 1.0e+07
30
Energy 20
15
10
5
0
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07
Time (s)
Figure 2.40 Energy balance for a repeated contact-contact release situation (tetrahedron with
initial velocity confined between two fixed tetrahedra).
reduces the complexity of the algebraic expressions used to evaluate the contact forces, as
discussed in Chapter 10. A further beneficial feature is a relationship between penetration
and mesh size by which the penalty parameters are given physical meaning, while the
effect of the penetration on the estimated domain fields can be controlled through mesh
refinement, i.e. in the same way as the accuracy of the finite element approximation itself.
2.7 ALTERNATIVE IMPLEMENTATION OF THE POTENTIAL
CONTACT FORCE
The finite element mesh is not the only way in which potential contact force can be defined.
One of the alternative ways of defining the contact force potential is to define the potential
over the domain of the discrete element irrespective of any finite element discretisation
employed. Such a potential for a discrete element in 2D is shown in Figure 2.41.