Page 84 - The Combined Finite-Discrete Element Method

POTENTIAL CONTACT FORCE IN 3D 67

32
30
28
× 1.0e+04 26 Legend:

24
Energy 22 Penalty = 1.0e+05
Penalty = 7.0e+05
20
18 Penalty = 1.0e+06
Penalty = 1.0e+07
16
0 0.005 0.01 0.015 0.02 0.025
Time (s)

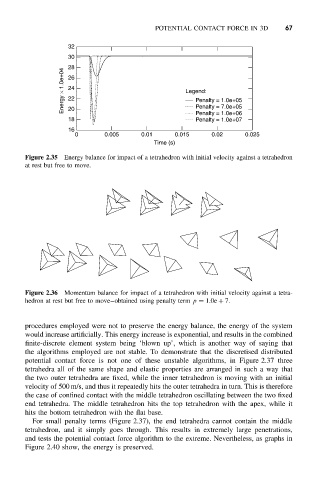
Figure 2.35 Energy balance for impact of a tetrahedron with initial velocity against a tetrahedron
at rest but free to move.

Figure 2.36 Momentum balance for impact of a tetrahedron with initial velocity against a tetra-
hedron at rest but free to move–obtained using penalty term p = 1.0e + 7.

procedures employed were not to preserve the energy balance, the energy of the system
would increase artificially. This energy increase is exponential, and results in the combined
finite-discrete element system being ‘blown up’, which is another way of saying that
the algorithms employed are not stable. To demonstrate that the discretised distributed
potential contact force is not one of these unstable algorithms, in Figure 2.37 three
tetrahedra all of the same shape and elastic properties are arranged in such a way that
the two outer tetrahedra are fixed, while the inner tetrahedron is moving with an initial
velocity of 500 m/s, and thus it repeatedly hits the outer tetrahedra in turn. This is therefore
the case of confined contact with the middle tetrahedron oscillating between the two fixed
end tetrahedra. The middle tetrahedron hits the top tetrahedron with the apex, while it
hits the bottom tetrahedron with the flat base.
For small penalty terms (Figure 2.37), the end tetrahedra cannot contain the middle
tetrahedron, and it simply goes through. This results in extremely large penetrations,
and tests the potential contact force algorithm to the extreme. Nevertheless, as graphs in
Figure 2.40 show, the energy is preserved.