Page 261 - The Mechatronics Handbook

0066_frame_C12 Page 26 Wednesday, January 9, 2002 4:22 PM

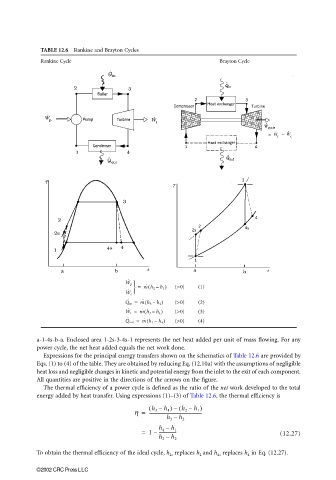
TABLE 12.6 Rankine and Brayton Cycles
Rankine Cycle Brayton Cycle

˙
W p 
 = m ˙ h 2 –( h 1 ) (>0) (1)
W c 
˙
(
˙
Q in = m ˙ h 3 – h 2 ) (>0) (2)
(
˙
W t = m ˙ h 3 – h 4 ) (>0) (3)
Q out = m ˙ h 1 – h 4 ) (>0) (4)
˙
(
a-1-4s-b-a. Enclosed area 1-2s-3-4s-1 represents the net heat added per unit of mass flowing. For any
power cycle, the net heat added equals the net work done.
Expressions for the principal energy transfers shown on the schematics of Table 12.6 are provided by
Eqs. (1) to (4) of the table. They are obtained by reducing Eq. (12.10a) with the assumptions of negligible
heat loss and negligible changes in kinetic and potential energy from the inlet to the exit of each component.
All quantities are positive in the directions of the arrows on the figure.
The thermal efficiency of a power cycle is defined as the ratio of the net work developed to the total
energy added by heat transfer. Using expressions (1)–(3) of Table 12.6, the thermal efficiency is
( h 3 – h 4 ) ( h 2 – h 1 )
–
h = -----------------------------------------------
h 3 – h 2
= 1 – h 4 – h 1 (12.27)
----------------
h 3 – h 2

To obtain the thermal efficiency of the ideal cycle, h 2s replaces h 2 and h 4s replaces h 4 in Eq. (12.27).

©2002 CRC Press LLC